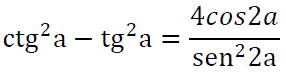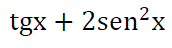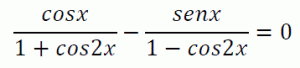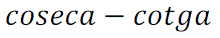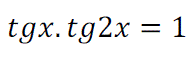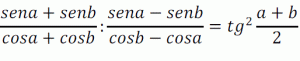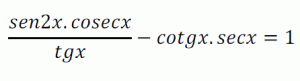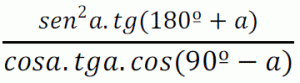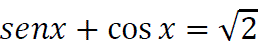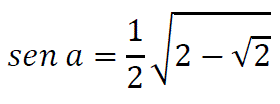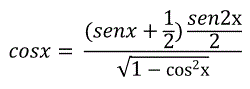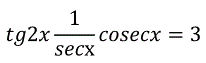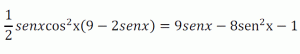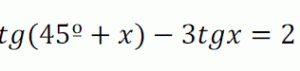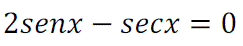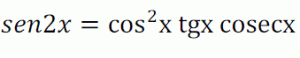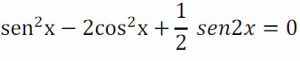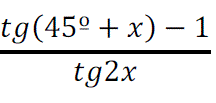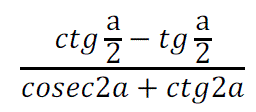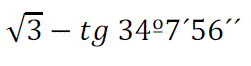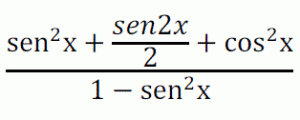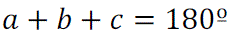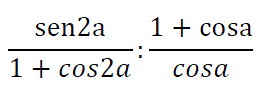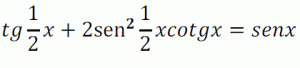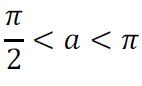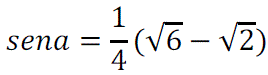Problema 222:
En un terreno horizontal hay una torre de 40 m de altura y distante 30 m del borde más próximo de un río. Desde lo alto de la torre se ve la anchura del río bajo un ángulo de 45º. Calcular el ancho del río.
Problema 221:
Determina los valores de x que verifican simultáneamente las igualdades:
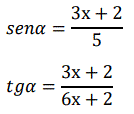
Problema 220:
La relación:

¿Es una identidad?
Problema 219:
Partiendo de la relación:

Comprueba que:

Problema 218:
Dada la función y= cos(-x) calcular el valor de la derivada de orden 22 en el punto de abscisa:
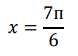
Problema 217:
Probar si es cierta la siguiente relación:
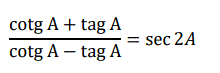
Problema 216:
Calcula sen a, sabiendo que la tg a= 0,782.
Problema 215:
María ve la parte superior de un árbol con un ángulo de elevación de 65°. Ella tiene una altura de 174 cm y se encuentra ubicada a 25 m del árbol.” ¿Cuál es el triángulo rectángulo que representa la situación?
Problema 214:
Simplificar:
Problema 213:
Simplificar:
Problema 212:
Si
¿cuánto vale
Problema 211:
Hallar la longitud del lado menor de un paralelogramo que tiene 480 m2 de área y sus diagonales miden 36 m y 30 m.
Problema 210:
Resolver un triángulo, sin recurrir a las tablas de logaritmos, en el que conocemos ;  y
y
Problema 209:
Trazar la gráfica de la función:
Problema 208:
Desde un cierto punto del suelo se ve el punto más alto de una torre formando un ángulo de 30º con la horizontal. Si nos acercamos 75 metros hacia el pie de la torre, este ángulo se hace de 60º. Hallar la altura de la torre.
Problema 207:
Los lados de un triángulo miden: 5 cm, 6 cm y 8 cm. Calcular el seno y el coseno del ángulo mayor.
Problema 206:
En el croquis de un viajero el punto A queda 5 km del punto B y el punto C queda a 7 km de B y a 8,4 km de A. Determinar
1.- Los ángulos A-B-C
2.- Conociendo que C = 31,5 grados; a = 4; b = 8, calcular B
3.- Conociendo A = 105 grados; b = 11; c = 8, calcular a.
Problema 205:
Uno de los lados de un triángulo es doble del otro, y el ángulo comprendido vale 60º. Hallar los otros dos ángulos. No usar ni tablas ni calculadora.
Problema 204:
Sabiendo que sen a= 3/5 y cos b= 4/5, hallar el valor del ángulo (a+b).
Problema 203:
En un triángulo, el lado a= 4m, y los ángulo B y C miden, respectivamente, 45º y 60º. Resolver el triángulo y hallar su área.
Problema 202:
De un triángulo ABC se conoce el ángulo A= 60º, y los lados AB= 12 cm y AC= 6 cm. Hallar el tercer lado y los otros dos ángulos del triángulo.
Problema 201:
Si a y b son los arcos comprendidos entre п/2 y п, y tales que cos a=-1/3 y sen b=1/2, ¿cuánto valdrá sen (a+b)?
Problema 200:
¿Por qué? Razona la respuesta.
Problema 199:
De estas igualdades, ¿cuáles son verdaderas y cuáles son falsas? Razona la respuesta.
Problema 198:
Sobre los lados de un hexágono regular se construyen cuadrados. Al unir los vértices de estos cuadrados se obtiene un dodecágono regular. Si el lado del hexágono mide 4 cm, calcular el área del dodecágono.
Problema 197:
En un hexágono regular ABCDEF, de 4 cm de lado, se trazan las diagonales AC y BD. Que se cortan en P. Calcular las medidas de los ángulos del triángulo ABP la las longitudes de los segmentos AP y PC.
Problema 196:
En un trapecio rectángulo, ABCD, Â= al ángulo D= 90º; el ángulo B= 45º. La diagonal AC es perpendicular al lado CB y mide 8 cm. Calcular el área del trapecio.
Problema 195:
Escríbase, en función de tg a y tg b, la siguiente expresión:
Problema 194:
Hallar el cociente simplificado, de la expresión:
Problema 193:
Reducir a cotg a/2 la siguiente expresión:
Problema 192:
Reducir la siguiente expresión a otra, en la que no figure más que tg δ y tg γ:
Problema 191:
Demostrar que se verifica la siguiente igualdad:
Problema 190:
Reducir a
La expresión siguiente:
Problema 189:
Demostrar que se verifica la siguiente igualdad:
Problema 188:
Demostrar que se verifica la siguiente igualdad:
Problema 187:
¿A qué línea trigonométrica del arco “a” equivale la expresión siguiente?
Problema 186:
Simplificar la expresión siguiente:
Problema 185:
Problema 184:
Demostrar que si a+b+c= 180º, se verifica la siguiente igualdad:
Problema 183:
En un hexágono regular calcula el ángulo del lado interior y el valor del ángulo que forman dos diagonales que salen del mismo vértice y llegan a otros dos consecutivos.
Problema 182:
Expresar en radianes los siguientes ángulos expresados en grados:
0º; 30º; 150º; 210º; 330º.
Problema 181:
El radio de un pentágono regular mide 20 m. Calcular el área de dicho pentágono.
Problema 180:
Demostrar que si a+b+c= 180º, se verifica:
Problema 179:
Simplificar la siguiente expresión:
Problema 178:
Hallar el valor de la expresión siguiente; para b= 45º:
Problema 177:
Transformar la expresión siguiente en otra que no figure más que sen a:
Problema 176:
Demostrar que se verifica la igualdad siguiente:
Problema 175:
¿A qué línea trigonométrica equivale la siguiente expresión?
Problema 174:
Demostrar que se verifica la igualdad siguiente:
Problema 173:
Escribir (sen a+ tg a)·(cos a + cotg a) en función de sen a y cos a.
Problema 172:
Simplificar la expresión siguiente:
Problema 171:
Simplificar la expresión siguiente:
Problema 170:
Demostrar que se verifica la igualdad siguiente:
Problema 169:
Demostrar que se verifica la igualdad siguiente:
Problema 168:
Simplificar la siguiente expresión:
Problema 167:
Calcula el valor de tg 2a.
Problema 166:
Halla el valor verdadero de la expresión siguiente para a= 90º
Problema 165:
Hallar el verdadero valor de la expresión siguiente, para x= 90º
Problema 164:
Si a+b= 90º, demostrar que se verifica la siguiente igualdad:
Problema 163:
Simplificar la siguiente expresión:
Problema 162:
Demostrar que la expresión:
Equivale a: 2·sen a· cos a
Problema 161:
Demostrar que se verifica la siguiente igualdad:
Problema 160:
Hallar el verdadero valor de la expresión siguiente; para a= 90º
Problema 159:
Reducir la siguiente expresión a una sola línea trigonométrica:
Problema 158:
Simplificar la expresión siguiente:
Problema 157:
Demostrar que se verifica la siguiente igualdad:
Problema 156:
Simplificar la siguiente expresión:
Problema 155:
Si a+b= 90º, demostrar que se verifica la siguiente igualdad:
Problema 154:
Simplificar la siguiente expresión:
Problema 153:
Demostrar que la expresión:
Equivale a:
Problema 152:
Demostrar que se verifica la siguiente igualdad:
Problema 151:
Escribir la siguiente expresión en función de “cos a” solamente:
Problema 150:
Simplificar la siguiente expresión:
Problema 149:
Transformar la siguiente expresión en otra que no figure más que tg x:
Problema 148:
Hallar el verdadero valor de la expresión siguiente, para a=45º:
Problema 147:
Desde la azotea de un edificio de 50 m de altura, Jorge observa simultáneamente un avión y un automóvil que se encuentra en una misma línea vertical el ángulo de elevación del avión es de 30º y el ángulo de depresión del auto es de 28º. Hallar la distancia horizontal del automóvil al pie del edificio y la altura del avión con respecto al automóvil.
Problema 146:
Un observador desde un helicóptero a 250 metros de altura sobre un lago ve dos barcas alineadas a un mismo lado de su vertical. ¿Cuál es la distancia entre ambas barcas, si los ángulos de depresión son 11° y 16°?
Problema 145:
Desde un punto el ángulo de elevación a la cima de una montaña es de 30° y el ángulo de elevación al extremo superior de una antena de altura 15 metros situada sobre la cima de la montaña de 45°. ¿Cuál es la altura de la montaña?
Problema 144:
Resolver un triángulo rectángulo, conociendo los radios de los círculos inscrito y circunscrito, r=3 m; y R=9 m.
Problema 143:
Calcular los elementos de un triángulo rectángulo, cuyo semiperímetro es de 136,69 m, y el radio del círculo circunscrito, de 58,90 m.
Problema 142:
La bisectriz correspondiente al ángulo B de un triángulo rectángulo, mide 341 m, y la hipotenusa, a= 598 m. Resolver el triángulo.
Problema 141:
Calcular los elementos de un triángulo rectángulo de 24 m2 de superficie, midiendo 2 m el radio del círculo inscrito.
Problema 140:
El perímetro de un triángulo rectángulo es de 10.219,56 m; y el radio del círculo inscrito mide 789,36 m. Resolver el triángulo.
Problema 139:
Resolver un triángulo rectángulo conociendo el radio del círculo inscrito r= 23,458 m; y la relación de los catetos, b/c=1/3
Problema 138:
Resolver un triángulo rectángulo con los datos siguientes: R= 38,456 m; B= 42º12´8´´,4.
Problema 137:
Resolver un triángulo rectángulo con los siguientes datos: b= 854,765 m; r= 200 m.
Problema 136:
Resolver un triángulo rectángulo de hipotenusa igual a 1515,25 m, circunscrito a un círculo de 214,25 m de radio.
Problema 135:
Resolver un triángulo rectángulo, sabiendo que la bisectriz de A divide a “a” en dos segmentos, que miden 182 m y 410 m.
Problema 134:
Calcular los elementos de un triángulo rectángulo, sabiendo que las proyecciones de los catetos b y c sobre la hipotenusa miden 3.596,32 m y 2.465,15 m, respectivamente.
Problema 133:
La hipotenusa de un triángulo rectángulo mide 104 m, y la altura que parte del vértice del ángulo recto, 40 m. Halla los valores de los ángulos agudos, siendo B>C
Problema 132:
Resolver el triángulo rectángulo de área igual a 73.926 m2, conociendo además la relación de un cateto y la hipotenusa, b/a=3/5.
Problema 131:
Calcular los elementos de un triángulo rectángulo, verificándose: a= 258 m; sen B= 2 sen C.
Problema 130:
Resolver un triángulo rectángulo de hipotenusa igual a 346 m, sabiendo que 2B= tg C.
Problema 129:
Resolver un triángulo rectángulo, sabiendo que se verifican las siguientes igualdades: b= sec C; c= cosec C.
Problema 128:
La hipotenusa de un triángulo rectángulo mide 1.915 m, y el producto de los catetos es igual a 48.764 m2. Determinar los ángulos agudos.
Problema 127:
Resolver un triángulo rectángulo de perímetro 72 m y b/c=2/3
Problema 126:
Resolver un triángulo rectángulo, conociendo c= 15,92 m y a/b=47/110
Problema 125:
Calcular los ángulos agudos de un triángulo rectángulo, verificándose que b/c=3/8.
Problema 124:
El perímetro de un triángulo rectángulo es de 140,88 m, y B=61º 10´4´´,8. Hallar los demás elementos.
Problema 123:
Resolver un triángulo rectángulo, conociendo un cateto, b=1270,353 m y la suma de la hipotenusa y el otro cateto. a+c=1719,817 m
Problema 122:
Dado a.b=4.271,56 m2; B=18º24´10´´,3. Resolver el triángulo.
Problema 121:
Calcular los ángulos de un triángulo rectángulo, verificándose la relación: b/c=2/3
Problema 120:
En una circunferencia de radio 6 cm trazamos una cuerda AB a 3 cm del centro. Halla el ángulo AOB.
Problema 119:
Calcula el ángulo que forma la tangente a las circunferencias de la figura con la línea que une sus centros. Los radios miden 4 y 9 cm, y la distancia entre sus centros es de 16 cm.
Problema 118:
Dos circunferencias son tangentes exteriormente y sus radios miden 9 metros y 4 metros, respectivamente. Halla el ángulo 2α que forman sus tangentes comunes.
Problema 117:
Dos circunferencias secantes tienen radios de 10 cm y 13 cm. Sus tangentes comunes forman un ángulo de 30º. Calcula la distancia entre los centros.
Problema 116:
Las tangentes a una circunferencia de centro O, trazadas desde un punto exterior, P, forman un ángulo de 50º. Halla la distancia PO sabiendo que el radio de la circunferencia es 12,4 cm.
Problema 115:
En un trapecio isósceles de bases AB y CD, conocemos los lados AB=5 m y BC=3√2 m, y los lados que forma la base mayor con los lados oblicuos, que son 45º. Halla su área.
Problema 114:
Calcula la altura QR, cuyo pie es inaccesible y más alto que el punto donde se encuentra el observador, con los datos de la figura.
Problema 113:
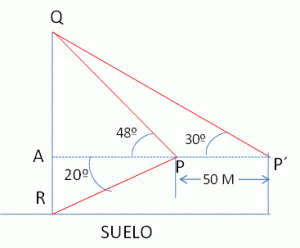
Halla la altura de la torre QR de pie inaccesible y más bajo que el punto de observación con los datos de la figura.
Problema 112:
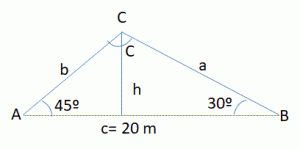
Para medir la altura de la montaña AB nos hemos situado en los puntos C y D distantes entre sí 250 metros, y hemos tomado las siguientes medidas: ACB= 60º; BCD= 65º; BDC= 80º. Calcula la altura de la montaña.
Problema 111:
Para hallar la altura de un globo, realizamos las mediciones indicadas en la figura. ¿Cuánto dista el globo del punto A?, ¿Cuánto del punto B? y ¿A qué altura está el globo?
Problema 110:
Para calcular la altura del edificio, PQ, hemos medido los ángulos que indica la figura. Sabemos que hay un funicular para ir de S a Q, cuya longitud es de 250 metros. Halla PQ.
Problema 109:
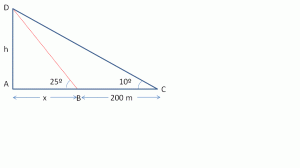
Calcula la altura de la luz de un faro sobre un acantilado cuya base es inaccesible, si desde un barco se toman las siguientes medidas:
El ángulo que forma la visual hacia la luz con la línea del horizonte es de 25º.
Nos alejamos 200 metros y el ángulo que forma ahora dicha visual es de 10º.
Problema 108:
Desde el lugar donde me encuentro, la visual de la torre forma un ángulo de 32º con la horizontal. Si me acerco 25 metros, el ángulo es de 50º. ¿Cuál es la altura de la torre?
Problema 107:
El lado de la base de una pirámide cuadrangular mide 6 metros y el ángulo APD 60º. Halla su volumen.
Problema 106:
Desde la torre de control de un aeropuerto se establece comunicación con un avión que va a aterrizar. En ese momento, el avión se encuentra a una altura de 1.200 metros y el ángulo de observación desde la torre (ángulo que forma la visual hacia el avión con la horizontal) es de 30º. ¿A qué distancia está el avión del pie de la torre si ésta mide 40 metros de altura?
Problema 105:
Halla “h”, “x” y “b”, según la figura.
Problema 104:
En dos comisarías de policía, A y C, se escucha la alarma de un banco B. Con los datos de la figura, calcula la distancia del banco a las dos comisarías.
Problema 103:
Conocemos la distancia de nuestra casa a la iglesia, 137 m; la distancia de nuestra casa al depósito de agua, 211 m; y el ángulo, 43º, bajo el cual se ve desde nuestra casa el segmento cuyos extremos son la iglesia y el depósito. ¿Qué distancia hay de la iglesia al depósito?
Problema 102:
En el triángulo ABC calcula “x”, “h” e “y”.
Problema 101:
En el triángulo ABC calcula h y a.
Problema 100:
De un triángulo rectángulo se sabe que su área es 864 cm2 y un cateto mide 48 cm. Calcula las razones trigonométricas de sus ángulos.
Problema 99:
Un avión vuela entre dos ciudades, A y B que distan 80 km. Las visuales desde el avión a A y B forman ángulos de 29º y 43º con la horizontal respectivamente. ¿A qué altura vuela el avión?
Problema 98:
Una escalera para acceder a un túnel tiene la forma y las dimensiones de la figura. Calcula la profundidad del punto B.
Problema 97:
Dos edificios distan entre sí 150 m. Desde un punto del suelo que está entre los dos edificios, vemos que las visuales a los puntos más altos de estos forman con la horizontal ángulos de 35º y 20º. ¿Cuál es la altura de los edificios, si sabemos que miden lo mismo?
Problema 96:
Dos antenas de radio están sujetas al suelo por cables tal como indica la figura. Calcula la longitud de cada uno de los tramos de cable y la distancia AE.
Problema 95:
Calcula la altura, h, del siguiente triángulo, según la figura anexa.
Problema 94:
Calcula la altura, h, del siguiente triángulo, según la figura anexa.
Problema 93:
Una estatua de 2,5 m está colocada sobre un pedestal. Desde un punto del suelo se ve el pedestal bajo un ángulo de 15º y la estatua bajo un ángulo de 401. Calcula la altura del pedestal.
Problema 92:
Hemos colocado un cable sobre un mástil que lo sujeta como indica el croquis. ¿Cuánto mide el cable y el mástil?
Problema 91:
Calcula el área del siguiente triángulo (ver croquis)
Problema 90:
Calcula el área del siguiente triángulo (ver croquis)
Problema 89:
Los brazos de un compás, que miden 12 cm, forman un ángulo de 50º. ¿Cuál es el radio de la circunferencia que puede trazarse con esa abertura?
Problema 88:
En un entrenamiento de fútbol se coloca el balón en un punto situado a 5 m y 8 m de cada uno de los postes de la portería, cuyo ancho es de 7 m. ¿Bajo qué ángulo se ve la portería desde ese punto?
Problema 87:
Para localizar una emisora clandestina, dos receptores, A y B, que distan entre sí 10 km, orientan sus antenas hacia el punto donde está la emisora. Estas direcciones forman con AB ángulos de 40º y 65º. ¿A qué distancia de A y B se encuentra la emisora?
Problema 86:
El lado de un rombo mide 8 cm y el ángulo menor es de 38º. ¿Cuánto miden las diagonales?
Problema 85:
Calcula los lados iguales y el área de un triángulo isósceles cuyo lado desigual mide 24 cm y el ángulo opuesto a la base mide 40º
Problema 84:
Una persona de 1,78 m de estatura proyecta una sombra de 66 cm, y en ese momento un árbol da una sombra de 2,3 m:
- ¿Qué ángulo forman los rayos del Sol con la horizontal?
- ¿Cuál es la altura del árbol?
Problema 83:
Al recorrer tres kilómetros por una carretera, hemos ascendido 280 m. ¿Qué ángulo forma la carretera con la horizontal?
Problema 82:
Si queremos que una cinta transportadora de 25 m eleve la carga hasta una altura de 15 m, ¿qué ángulo se deberá inclinar la cinta?
Problema 81:
De un triángulo isósceles conocemos su lado desigual, 18 m; y su altura, 10m. ¿Cuánto miden sus ángulos?
Problema 80:
Una escalera de pared de 3m está apoyada en una pared. ¿Qué ángulo forma la escalera con el suelo si su base está a 1,2 m de la pared?
Problema 79:
Cuando los rayos del sol forman 40º con el suelo, la sombra de un árbol mide 18 m. ¿Cuál es su altura?
Problema 78:
La longitud del lado de un octógono regular es 12 cm. Halla los radios de las circunferencias inscrita y circunscrita al octógono.
Problema 77:
La longitud del lado de un octógono regular es 8 cm. Halla los radios de las circunferencias inscrita y circunscrita al octógono.
Problema 76:
Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 30º y si nos acercamos 10 m, bajo un ángulo de 60º.
Problema 75:
Calcular la altura de un árbol con los siguientes datos:
Altura de la vara: 124 cm
Sombra de la vara: 37 cm
Sombra del árbol: 258 cm
Problema 74:
En una ruta de montaña, una señal indica una altitud de 785 m. Tres kilómetros más adelante, la altitud es de 1.265 m. Halla la pendiente media de esa ruta y el ángulo que forma con la horizontal.
Problema 73:
Una señal de peligro en una carretera nos advierte que la pendiente es del 12%. ¿Qué ángulo forma ese tramo de la carretera con la horizontal? ¿Cuántos metros hemos descendidos después de recorrer 7 km por esa carretera?
Problema 72:
Calcular el área de una parcela triangular, sabiendo que sus dos lados miden 80 m y 130 m, y forman entre ellos un ángulo de 70º.
Problema 71:
Un barco pide socorro y se reciben sus señales en dos estaciones de radio, A y C, que distan entre sí 50 km. Desde las estaciones se miden los siguientes ángulos: BAC= 46º y BCA= 53º. ¿A qué distancia de cada estación se encuentra el barco?
Problema 70:
Hallar el radio de una circunferencia sabiendo que la cuerda de 24,6 m tiene como arco correspondiente uno de 70º.
Problema 69:
Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12º. ¿A qué distancia se halla el pueblo?
Problema 68:
Un árbol de 50 m de alto proyecta una sombra de 60 m de larga. Encontrar el ángulo de elevación del sol en ese momento.
Problema 67:
Para determinar la altura de un poste nos hemos alejado 7 m de su base y hemos medido el ángulo que forma la visual al punto con la horizontal, obteniendo un valor de 40º. ¿Cuánto mide el poste?
Problema 66:
Dado el triángulo de la figura, calcula:
- La proyección de MN sobre MP.
- La altura correspondiente a la base MP.
- El área del triángulo.
Problema 65:
Calcula, aplicando el teorema de Pitágoras:
- Los lados iguales de un triángulo rectángulo isósceles cuya hipotenusa mide 1
- La altura de un triángulo equilátero de lado 1
Problema 64:
Bernardo ve desde su casa el castillo y la abadía. Conoce las distancias a ambos lugares, y quiere averiguar la distancia del castillo a la abadía.
Problema 63:
Bernardo conoce la distancia AB a la que está el árbol y los ángulos CBA y BAC; y quiere calcular la distancia BC a la que está Carmen.
Problema 62:
Al estar ubicados en la parte más alta de un edificio se observan dos puntos A y B en el suelo con un ángulo de depresión de 37º y 53º. Se pide hallar la distancia entre los dos puntos si la altura del edificio es 120 m.
Problema 61:
En la maniobra de aproximación de un avión hacia un aeropuerto, el piloto debe reportar a la torre el inicio del descenso cuando los ángulos con que ve la cabecera y el final de la pista (respecto a la horizontal) son 60° y 30° respectivamente. La pista mide 2,5 km. ¿A qué altura se encuentra el avión cuando el piloto reporta el inicio del descenso?
b. Si se duplica la longitud de la pista, ¿a qué altura se debe reportar el inicio del descenso?
Problema 60:
Ana observa la parte superior de una torre con un ángulo de elevación de 37 grados. Camina 28 m hacia la torre y la vuelve a observar, pero ahora con un ángulo de elevación de 53 grados. Si emplea 12 segundos en llegar al pie de la torre, halla la velocidad a la que se ha desplazado.
Problema 59:
Se da b=891,15 m, y se sabe que sen B= tg C. Calcular c.
Problema 58:
a/b=5/3, c= 40 m. Con estos datos, resolver el triángulo.
Problema 57:
Resolver un triángulo rectángulo con los siguientes datos:
a= 2854,37 m, B/C=1/7
Problema 56:
Conociendo a= 578,252 m, y C-B=12º17´20´´, resolver el triángulo.
Problema 55:
Resolver un triángulo rectángulo, dados b= 0,248 m., y a= sen C
Problema 54:
Resolver un triángulo rectángulo, dado un cateto, b= 320 m., y el ángulo opuesto B= 52º30´.
Problema 53:
La hipotenusa de un triángulo rectángulo mide 6061,47m., y un cateto b= 4668,937 m. Calcular los demás elementos.
Problema 52:
a=1915 m y B=45´43´´. Hallar el área del triángulo.
Problema 51:
a=3827,55 m y B=1,2 radianes; calcular b y c
Problema 50:
a=2961,35 m y B=90g 5142; calcular los demás elementos del triángulo rectángulo.
Problema 49:
Conociendo a=150 m y B=36º52´11´´,6; calcular los demás elementos del triángulo rectángulo
Problema 48:
Una torre se inclina 5º hacia el lado contrario al sol, proyecta una sombra de 50 m cuando el ángulo de elevación del astro es de 58º ¿Cuál es la altura de la torre?
Problema 47:
Un cuadro localizado sobre una pared es tal que su borde inferior está a una distancia de 20 cm sobre el nivel del ojo del observador situado a 200 cm de la pared. Si el ángulo que forman las visuales con los bordes inferior y superior, respectivamente, mide 10º. ¿Cuál es la altura del cuadro?
Problema 46:
La sombra de un árbol mide 50 m y el ángulo que forman los rayos del sol con el suelo es de 60º. ¿Cuál es la altura del árbol?
Problema 45:
Una escalera de 12 metros de largo está apoyada en una pared con un ángulo de 60º respecto al suelo. Calcular hasta altura de la pared hasta donde apoya la escalera, y la separación de ésta a la pared.
Problema 44:
Calcular la altura del pico de una montaña, sabiendo que, en ese momento del día, el Sol incide con sus rayos sobre el suelo con un ángulo de 75º y provoca una sombra sobre el suelo de 53 metros.
Problema 43:
Con los datos que se acotan en la figura, calcular la longitud de AB
Problema 42:
En un triángulo isósceles los dos lados iguales miden 10 cm y su área vale 48 cm2. Calcula el valor de sus ángulos
Problema 41:
En un terreno horizontal se divisa una torre desde un punto A bajo un ángulo de 30º. Si nos aproximamos 20 m se llega a un punto B, desde el que observamos la torre bajo un ángulo de 45º. Calcula la altura de la torre.
Problema 40:
Demostrar que se verifica la siguiente igualdad:
Problema 39:
Transformar la expresión
En otra calculable por logaritmos
Problema 38:
Resolver
Problema 37:
Simplificar la siguiente expresión:
Problema 36:
Expresar
En función de
Problema 35:
Resolver la ecuación siguiente, para valores de x comprendidos entre 0º y 180º
Problema 34:
Demostrar que se verifica la siguiente igualdad:
Problema 33:
Obtener todas las soluciones de la siguiente ecuación, y deducir las válidas
Problema 32:
Deducir tgx de la ecuación:
Problema 31:
Resolver:
Problema 30:
Resolver:
Problema 29:
Simplificar la expresión
Problema 28:
Resolver
Problema 27:
Sabiendo que
Hallar tg 2a
Problema 26:
Resolver:
Problema 25:
Resolver:
Problema 24:
Hallar el valor de x, menor que un cuadrante, que satisface a la ecuación:
Problema 23:
Resolver la siguiente ecuación, siendo x menor que un cuadrante:
Problema 22:
Resolver la ecuación:
Problema 21:
Resolver la ecuación:
Problema 20:
Resolver la ecuación:
Problema 19:
Simplificar la siguiente expresión:
Problema 18:
Hallar el verdadero valor de la expresión siguiente, para x=90º
Problema 17:
Simplificar la expresión
Problema 16:
Transformar la expresión
en otra calculable por logaritmos.
Problema 15:
Transformar la siguiente expresión en otra que no figure más que tg a
Problema 14:
Demostrar que si
Se verifica la siguiente igualdad:
Problema 13:
Hallar el valor de la siguiente expresión
Problema 12:
Transforma la expresión que se cita a continuación en otra calculable por logaritmos:
Problema 11:
Sabiendo que cosa= 0,62. Hallar el valor de cosa/2, siendo
Problema 10:
Simplifica:
Problema 9:
Hallar, en función de m, los valores de las demás líneas trigonométricas del arco a. Siendo tga = m.
Problema 8:
Demostrar que se verifica la igualdad siguiente
Problema 7:
Si se verifica que
y sen a=2/3, ¿cuál es el valor de sec2a?
Problema 6:
Sabiendo que
Calcular el valor de cotg 2a
Problema 5:
Sabiendo que sen 30º= 1/2, hallar el valor, aproximado en milésimas, del seno de 75º
Problema 4:
Cotg x= 2,84. Calcular el valor, aproximado en milésimas, de la cosecante del mismo arco.
Problema 3:
Hallar los valores de las líneas trigonométricas del arco de 240º, sin recurrir a las tablas.
Problema 2:
Dado sen x=3/5, determinar los valores de las demás líneas trigonométricas del arco x.
Problema 1:
Sabiendo que el coseno de un arco comprendido entre 270º y 360º tiene por valor 0,4004, calcular los valores aproximados en milésimas, de las demás líneas trigonométricas.