Problema 235:
Las edades de tres hermanos, sumadas dos a dos, dan cinco, siete y ocho años, respectivamente. Hallar la edad de cada hermano.
Problema 234:
En las ecuaciones:
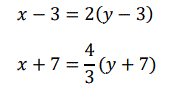
“x” e “y” representan, respectivamente las edades de Carlos y de Antonio. Enuncia el problema que originan estas ecuaciones.
Problema 233:
Juan, Pedro y Marcos tienen entre los tres sesenta y tres años. Si Juan tuviera tres años menos su edad sería el doble de las edades de Pedro y Marcos juntos. Si Pedro tuviera un año más su edad sería la mitad de la de Marcos. ¿Qué edad tienen actualmente cada uno de ellos?
Problema 232:
Dentro de 4 años la edad de A será el triplo de la de B, y hace dos años era el quíntuplo. Hallar las edades actuales.
Problema 231:
Hace 5 años la edad de un padre era tres veces la de su hijo, y dentro de 5 años será el doble. ¿Qué edades tienen ahora el padre y el hijo?
Problema 230:
Si hubiera nacido 15 años antes, entonces lo que me faltaría actualmente para cumplir 78 años, sería los cincos tercios de la edad que tendría si hubiese nacido 7 años después. ¿Qué edad tendré dentro de 5 años?
Problema 229:
Las edades de dos amigos suman 42 años. ¿Cuál es la edad de cada uno sabiendo que el mayor tiene 5/3 de la edad del menor menos 6 años?
Problema 228:
Hállese la edad de una persona, sabiendo que si se añaden dos años a la cuarta parte da lo mismo que si se quitan 4 de 1/3 de edad.
Problema 227:
¿Cuál es la edad de un niño sabiendo que si del doble de su edad se le resta el triple de la que tenía hace 4 años, se tiene la edad actual?
Problema 226:
Un padre tiene 34 años y su hijo 13. ¿Dentro de cuántos años la edad del padre será el doble de la edad del hijo?
Problema 225:
Un padre tiene 45 años y su hijo 11. ¿Dentro de cuánto tiempo la edad del padre será el triple de la edad del hijo?
Problema 224:
La suma de las edades de tres niños es de 27 años. El mayor tiene 5 años más que el mediano, y éste 2 años más que el menor. ¿Cuál es la edad de cada uno?
Problema 223:
En una familia la suma de las edades de los 4 hijos es 28 años. Cuál es la edad de cada uno si el mayor tiene 4 años más que el 2º, el segundo 2 años más que el 3º y éste 4 más que el pequeño.
Problema 222:
Preguntado un padre por la edad de su hijo contesta: “si del doble de los años que tiene se quitan el triple de los que tenía hace 6 años se tendrá su edad actual” ¿Qué edad tiene el hijo?
Problema 221:
La edad de un padre y la edad de su hijo suman 100 años. Cuando el padre tenía la edad que ahora tiene el hijo, ambas edades sumaban 52 años. Calcula la edad de cada uno.
Problema 220:
Una señora tiene 70 años, y su hijo exactamente la mitad de esa edad. ¿Cuántos años han pasado desde que la madre tenía una edad igual a
veces la edad de su hijo?
Problema 219:
Hace cuatro años un individuo tenía la mitad más la tercera parte de la edad que tiene hoy. ¿Cuál es su edad?
Problema 218:
Un padre tiene seis veces la edad de su hijo, y la suma de las dos edades es 91. ¿Cuántos años tiene cada uno?
Problema 217:
Un padre tiene el triple de la edad de su hijo. Si el padre tuviese 30 años menos y el hijo 8 años más, los dos tendrían la misma edad. Hallar la edad del padre y del hijo.
Problema 216:
La suma de las edades de tres personas es de 100 años; la mediana tiene 10 años más que la joven, y la mayor tiene tantos como las otras dos juntas. ¿Qué edad tiene cada una?
Problema 215:
Dentro de 2 años la edad de una persona será el triple de la otra, y dentro de 14 años solo será el doble. ¿Cuál es la edad de cada una?
Problema 214:
Cuando a un padre le preguntaron por la edad de su hija, respondió en estos términos: “Si al doble de los años que tiene mi hija se le quita el triple de los que tenía hace 6 años, se obtiene la edad actual”. Halla la edad actual de la hija.
Problema 213:
La edad de Julio es de 40 años, y la de sus tres hijos es de 10 años, 7 años y 3 años. ¿Dentro de cuántos años la edad del padre será igual a la suma de las edades de los hijos?
Problema 212:
Pedro tiene 10 años y su madre 42. ¿Dentro de cuántos años la edad de la madre será el triple de la de Pedro?
Problema 211:
Hace 12 años, la edad de un hombre era el cuádruple de la de su hija. Sabiendo que el padre tenía 27 años cuando nació su hija, halla las edades actuales de ambos.
Problema 210:
Laura tiene 30 años menos que su padre, y éste tiene el cuádruple de los años que su hija. Halla la edad de cada uno.
Problema 209:
La edad de Pedro excede en 5 unidades al doble de la edad de Elisa. Hace diez años Pedro tenía el triple de edad que Elisa. ¿Cuáles son las edades respectivas de Pedro y Elisa?
Problema 208:
La edad de Enrique es la mitad de la edad de Pedro; y la de Juan el triplo de la de Enrique, y la de Eugenio el doble de la de Juan Si las cuatro edades suman 132 años, ¿qué edad tiene cada uno?
Problema 207:
Melisa tiene el triple de edad que su hija Marta. Calcula la edad de cada una sabiendo que, dentro de 12 años, la edad de Melisa será solamente el doble de la de Marta.
Problema 206:
Juan tiene 28 años menos que su padre y 24 años más que su hijo. ¿Cuál será la edad de cada, sabiendo que entre los tres suman 100 años?
Problema 205:
Juanjo tiene el doble de edad de Raúl. Laura tiene tres años más que Juanjo. Si la suma de todos ellos es 58, ¿cuál es la edad de cada uno?
Problema 204:
La edad de un hijo es la quinta parte de la edad de su padre, y dentro de siete años el padre tendrá el triple de la edad de su hijo. Calcula las edades de cada uno.
Problema 203:
Un padre tiene 37 años y las edades de sus hijos suman 25. ¿Dentro de cuántos años las edades de los hijos sumarán como la edad del padre?
Problema 202:
La suma de las edades de los cuatro miembros de una familia es 104 años. El padre tiene 6 años más que la madre, que tuvo a los dos hijos gemelos a los 27 años. ¿Qué edad tiene cada uno?
Problema 201:
Antonio tiene 15 años, su hermano Roberto, 13, y su padre 43. ¿Cuántos años han de transcurrir para que entre los dos hijos igualen la edad del padre?
Problema 200:
El hermano mayor de una familia con tres hermanos tiene 4 años más que el segundo y éste 3 más que el menor. Si entre todos tienen la edad del padre que tiene 40 años, ¿qué edad tiene cada hermano?
Problema 199:
¿Cuál es la edad de Juan, si sabemos que el número que expresa sus años es igual a seis veces la suma de sus dos cifras, y que hace nueve años su edad se expresaba con las mismas cifras?
Problema 198:
Una señora tiene 70 años, y su hijo exactamente la mitad de esa edad. ¿Cuántos años han pasado desde que la madre tenía una edad igual a 3 1/3 veces la edad de su hijo?
Problema 197:
Las edades de dos amigos suman 42 años. ¿Cuál es la edad de cada uno sabiendo que el mayor tiene 5/3 de la edad del menor menos 6 años?
Problema 196:
Un padre tiene seis veces la edad de su hijo, y la suma de las dos edades es 91. ¿Cuántos años tiene cada uno?
Problema 195:
Un padre tiene el triple de la edad de su hijo. Si el padre tuviese 30 años menos y el hijo 8 años más, los dos tendrían la misma edad. Hallar la edad del padre y del hijo.
Problema 194:
Dentro de once años la edad de Pedro será la mitad del cuadrado de la edad que tenía hace 13 años. Calcula la edad de Pedro.
Problema 193:
Un padre dice a su hijo: ”Hoy tu edad es 1/5 de la mía, y hace siete años no era más que 1/9”. Halla las edades del padre y de su hijo.
Problema 192:
Las tres cuartas de la edad de una persona A exceden en quince años a la de B. Hace cuatro años la edad de A era doble de la de B. Halla la edad de cada una.
Problema 191:
Preguntada una persona por su edad responde: ”Si del cuadrado de mi edad se quitan 2/3; 3/4 y 11/6 de la misma, lo que resta es igual a 20 veces mi edad más 18. Hallar su edad.
Problema 190:
Preguntada una persona por su edad responde: ”Si del cuadrado de mi edad se quitan 2/3; 3/4 y 11/6 de la misma, lo que resta es igual a 20 veces mi edad más 18. Hallar su edad.
Problema 189:
Hace cuatro años las edades de dos personas estaban en la relación de 2 es a 3. Dentro de cuatro años estarán en la relación de 4 es a 5. ¿Qué edades tienen esas personas?
Problema 188:
La edad de un hijo más la tercera parte de la edad de su padre suman 22 años. Dentro de seis años, la edad del padre excederá al duplo de la edad del hijo en diez años. ¿Cuál es la edad actual de ambos?
Problema 187:
Hallar las edades de dos individuos sabiendo que la edad del primero hace 5 años era la mitad de la edad que hoy tiene el segundo, y dentro de cinco años el más viejo solo sacará cinco años al más joven.
Problema 186:
La suma de nuestras edades es 108 y su cociente es 5. ¿Cuántos años tenemos?
Problema 185:
¿Cuál es la edad actual de un padre que duplica la de su hijo, y que hace 24 años su edad era 10 veces mayor que la de su hijo?
Problema 184:
Yo tengo 18 años más que tú. Hace 18 años mi edad era los 5/2 de la tuya. ¿Qué edades tenemos ambos?
Problema 183:
La edad de Juan es triple que la de Alberto, y dentro de 20 años será el doble. Hallar las edades de ambos.
Problema 182:
La edad de un hijo es los dos quintos de la edad de su padre. Hace ocho años la edad del hijo era los dos séptimos de la edad del padre. Hallar las edades actuales de ambos.
Problema 181:
Hace un año la edad de un padre era 3 veces mayor que la del hijo, pero dentro de 13 años no tendrá más que el doble. Halla las edades del padre y del hijo.
Problema 180:
Hace dos años un padre tenía el triple de la edad de su hijo, y dentro de once solo tendrá el doble. Hallar la edad que tienen ahora.
Problema 179:
Hace 18 años la edad de una persona era doble de la otra. Dentro de nueve años la edad de la primera será solamente los 5/4 de la segunda. ¿Cuáles son sus edades actuales?
Problema 178:
La edad de María es doble que la edad de Julia. Hace 10 años la suma de las edades de las dos era igual a la edad actual de María. ¿Cuál es la edad actual de María?
Problema 177:
La edad de Pedro era doble que la edad de Luis hace un año. Cuando pasen nueve años, la edad de Pedro será 4/3 de la edad de Luis. ¿Qué edad tiene actualmente cada uno?
Problema 176:
La edad de un padre es cuatro veces mayor que la edad de su hijo, pero hace seis años la edad del padre era siete veces mayor. ¿Cuál es la edad actual de ambos?
Problema 175:
La edad de un padre es hoy tres veces la de su hijo, y hace seis años era cinco veces la edad del hijo. ¿Cuántos años tiene cada uno?
Problema 174:
La edad de un hijo es la quinta parte de la edad de su padre, y dentro de siete años el padre tendrá el triple de la edad de su hijo. Calcula las edades de cada uno.
Problema 173:
Un hijo tiene treinta años menos que su padre, y éste tiene cuatro veces la edad del hijo. ¿Qué edad tiene cada uno?
Problema 172:
La edad de un padre es doble que la edad de su hijo. Hace diez años la edad del padre era triple que la edad del hijo. ¿Cuáles son las edades actuales del padre y del hijo?
Problema 171:
Un hombre dice: ”Si al doble de mi edad le restamos 17 años, obtenemos lo que me falta para tener 100 años”. ¿Qué edad tiene?
Problema 170:
Hace 10 años mi edad era los tres quintos de la edad que tendré dentro de 20 años. ¿Cuál es mi edad actual?
Problema 169:
Una madre y sus dos hijos tienen en conjunto 60 años. Halla la edad de cada uno sabiendo que el hijo mayor tiene 3 veces la edad del menor, y que la madre tiene el doble de la suma de las edades de los hijos.
Problema 168:
La suma de las edades de tres personas es 100 años. Halla la edad de cada una sabiendo que la mediana tiene 10 años más que la menor, y que la mayor tiene tantos años como las otras dos juntas.
Problema 167:
Yo tengo 52 años y tú 48 años. ¿Cuántos años hace que tu edad era los 9/10 de la mía?
Problema 166:
Un padre tiene 37 años y las edades de sus tres hijos suman 25. ¿Dentro de cuántos años las edades de los hijos sumarán como la edad del padre?
Problema 165:
Un padre tiene 42 años y su hijo 7. ¿Dentro de cuánto tiempo la edad del hijo será la cuarta parte de la del padre?
Problema 164:
Un padre tiene 60 años y sus dos hijos 16 y 14 años, respectivamente. ¿Dentro de cuántos años la edad del padre será igual a la suma de las edades de sus hijos?
Problema 163:
¿Cuál es la edad de un niño sabiendo que si del duplo de su edad se le resta el cuádruple de la que tenía hace tres años, se tiene la edad actual?
Problema 162:
Preguntado un padre por la edad de su hijo, contesta: ”Si del doble de los años que tiene se le quitan el triple de los que tenía hace seis años, se tendrá su edad actual”. Hallar la edad del hijo en el momento actual.
Problema 161:
Cuatro alumnos tienen juntos 50 años. Hallar sus edades respectivas sabiendo que cada uno tiene 3 años más que el que le sigue en edad.
Problema 160:
Una señora tiene 70 años, y su hijo exactamente la mitad de esa edad. ¿Cuántos años han pasado desde que la madre tenía una edad igual a 1 1/3 veces la edad de su hijo?
Problema 159:
La edad de un padre y la edad de su hijo suman 100 años. Cuando el padre tenía la edad que ahora tiene el hijo, ambas edades sumaban 52 años. Calcula la edad de cada uno.
Problema 158:
María le dice a Teresa: “Mi edad es 30 años y es el triple de la edad que tú tenías cuando yo tenía la edad que tú tienes actualmente”. ¿Cuál es la edad de Teresa?
Problema 157:
La suma de nuestras edades es 48 años. Dentro de 10 años la diferencia de nuestras edades será 16 años. ¿Cuál es la edad del mayor?
Problema 156:
La edad de Miluska es actualmente el quíntuple de la edad de su hijo. Si dentro de 5 años su edad será el triple de la edad que tendrá su hijo en ese tiempo. ¿Qué edad tenía Miluska cuando nació su hijo?
Problema 155:
Mi hermano mayor nació 8 años antes que yo. Si dentro de 10 años nuestras edades sumarán 82 años, ¿cuál es la edad de mi hermano mayor?
Problema 154:
Si al restarle el cuádruple de la edad que mi hija tenía hace 8 años del quíntuple de la edad que ella tendrá dentro de 2 años, se obtiene como resultado el triple de su edad. ¿Qué edad tiene mi hija?
Problema 153:
Actualmente mi edad es la cuarta parte de la edad que tendré dentro de 45 años. ¿Qué edad tengo actualmente?
Problema 152:
Halla la edad de Gisela, sabiendo que si a la tercera parte de la edad que tendrá dentro de 3 años le restamos la tercera parte de la edad que tenía hace 3 años, se obtiene como resultado la novena parte de su edad actual.
Problema 151:
La edad de Norka es el triple de la edad de Alberto. Hace cuatro años la suma de sus edades era la mitad de la edad que tendrá Norka dentro de catorce años. ¿Cuántos años tiene Norka?
Problema 150:
La edad de Nancy es el doble de la edad que Luis tenía hace 4 años. Si la edad actual de Luis y la que tendrá Nancy dentro de 5 años suman 39 años. ¿Cuántos años tuvo Nancy cuando Luis nació?
Problema 149:
La suma de los dígitos de la edad del padre de Lucía es igual a la edad de ella, si la edad de Lucía es la cuarta parte de la edad de su padre. ¿Cuántos años tiene cada uno?
Problema 148:
Una persona en 1996 tenía tantos años como lo indicaba el número formado por las dos últimas cifras del año de su nacimiento. ¿Qué edad tenía en 1987?
Problema 147:
En 1993 la edad de una persona era igual a la suma de las cifras del año en que nació. ¿Qué edad tendrá en el año 2000?
Problema 146:
Al preguntarle la edad de Guadalupe ella respondió: “Si al año en que cumplí los 18 años le suman el año en que cumplí los 23 años y le restan el año en que nací y el actual, obtienen 17 años”. La suma de las cifras de la edad de Guadalupe es:
Problema 145:
Patty le dice a Verónica: “Tú edad es el doble de aquella que tenías, cuando yo tuve el doble de edad que tú tuviste, cuando cumplí 4 años. Si nuestras edades actuales suman 32 años”. ¿Qué edad tengo?
Problema 144:
Gildeer le dice a Arturo: “Yo tengo el doble de la edad que tú tenías, cuando yo tenía la edad que tú tienes y cuando tu tengas mi edad, la suma de nuestras edades será 63 años”. ¿Qué edad tiene Arturo?
Problema 143:
Yo tengo el triple de la edad que tú tenías, cuando yo tenía la edad que tú tienes, y cuando yo tenga el triple de la edad que tú tenías hace 6 años, tú tendrás 72 años. ¿Cuántos años tenía uno de ellos cuando el otro nació?
Problema 142:
Las edades del profesor, tutor y alumno están en la relación de 5, 4 y 3 respectivamente. Hace 10 años las edades del tutor y alumno sumaban la mitad de lo que el profesor tendrá dentro de catorce años. ¿Cuánto suman las edades de los tres actualmente?
Problema 141:
La edad que tendrá Lulú dentro de 15 años y la edad que tenía hace “x” años están en la relación de 17 es a 11; mientras que la que tendrá dentro de “x” años y la edad que tenía hace 10 años están en la relación de 3 a 2. Hallar “x”
Problema 140:
Hace 2 años tenía la cuarta parte de la edad que tendré dentro de 22 años. ¿Dentro de cuántos años tendré el doble de la edad que tenía hace 5 años?
Problema 139:
Hace 10 años tenía la mitad de la edad que tendré dentro de 8 años. Dentro de cuántos años tendré el doble de la edad que tuve hace 8 años.
Problema 138:
La suma de las edades de Anya, Uriel y Fernando es de 60 años. Anya es mayor que Uriel por el mismo número de años que Uriel es mayor que Fernando. Cuando Uriel tenga la edad de Anya tiene ahora, ésta triplicará la que Fernando tiene en la actualidad. ¿Cuáles son sus edades?
Problema 137:
Cuando yo tenía un año menos de la edad que tú tienes, tú tenías 5 años menos de la edad que yo tengo. Pero cuando tengas mi edad nuestras edades sumarán 52 años. ¿Qué edad tiene mi esposa si nació 5 años después que yo?
Problema 136:
Dentro de 8 años la suma de nuestras edades será 46 años; pero hace “m” años la diferencia de nuestras edades era de 4 años. ¿Hace cuántos años la edad de uno era el triple de la del otro?
Problema 135:
Actualmente las edades de Ximena y Sheila suman 26 años. Sheila nació cuando Ximena tenía la mitad de los años que Sheila tendrá dentro de 2 años. ¿Cuántos años tiene Ximena?
Problema 134:
Si juntamos las edades de Juan y Pedro dentro de 8 años solamente obtendríamos 64. Al acercarse María, Juan le dice: “Cuando tú naciste yo tenía 4 años, pero cuando Pedro nació tú tenías 2 años” ¿Cuál es la edad de María?
Problema 133:
La edad de un padre sobrepasa en 5 años a la suma de las edades de sus tres hijos. Dentro de 10 años él tendrá el doble de la edad que tendrá el hijo mayor, dentro de 20 años tendrá el doble de la edad que tendrá el segundo y dentro de 30 años tendrá el doble de la edad que tenga el tercero. Hallar la edad del padre.
Problema 132:
Evelyn le dice a Isela: “Cuando yo tenga la edad que tú tienes, tu edad será 2 veces la que tengo y sabes que cuando tenía 10 años, tú tenías la edad que tengo”. ¿Cuánto suman sus edades actuales?
Problema 131:
Yo tengo el doble de la edad que tú tenías, cuando yo tenía la edad que tú tienes y cuando tú tengas la edad que yo tengo, mi edad será 30 años. ¿Qué edad tengo?
Problema 130:
Luis cuenta que cuando cumplió años en 1994, descubrió que su edad era igual a la suma de las cifras del año de su nacimiento. ¿Cuántos años tenía en 1979?
Problema 129:
Si 3 veces la edad de mi hermana es 2 veces mi edad, y hace 3 años 3 veces su edad era la mía. ¿Cuántos años tengo?
Problema 128:
“Paul le dice a Luigui: cuando tengas lo que yo tengo, es decir el triple de lo que tenías cuando yo tenía 4 años menos de los años que tienes, nuestras edades sumarán 68 años. Luigui a su vez le dice a Jorge: “cuando tengas lo que yo tengo, yo tendré como cinco veces lo que tenías cuando yo tenía lo que tú tienes”. ¿Qué edad tendrá Jorge cuando Paul tenga el triple de lo que tiene actualmente?
Problema 127:
Yo tengo el triple de la edad que tú tenías, cuando yo tenía la mitad de la edad que tú tienes y cuando tú tengas la edad que yo tengo, yo tendré el doble de la edad que tenía hace 12 años. ¿Cuánto suman nuestras edades actuales?
Problema 126:
Un coche tiene ahora la mitad de años que tenía Luis, cuando el coche era nuevo. ¿Cuántos años tiene el coche, si actualmente Luis tiene 12 años?
Problema 125:
Las edades de dos personas hace “n” años estaban en relación de 1 a 3, actualmente sus edades están en relación de 4 a 7. Si dentro de “2n” años sus edades sumarán 126. Halle la suma de sus edades dentro de “n” años.
Problema 124:
Kelly le dice a Marisela: cuando yo tenía tu edad, Andrea tenía 10 años. Marisela le responde: cuando yo tenga tu edad, Andrea tendrá 26 años. Andrea dice: Si sumamos los años que ustedes me llevan de ventaja, resultará el doble de mi edad. ¿Cuál es la edad de la mayor?
Problema 123:
Anita le dice a Rafaela: Hace 21 años mi edad era la mitad de la edad que tú tendrás dentro de 4 años, cuando yo tenga el doble de la edad que tú tienes. ¿Qué edad tiene Anita?
Problema 122:
Rommel dice: “Yo tengo 30 años y mi edad es el séxtuplo de la edad que tú tenías cuando yo tenía el cuádruplo de la edad que tú tienes. ¿Cuántos años tienes?
Problema 121:
Liliana tuvo a los 16 años quintillizos. Hoy las edades de los 6 suman 88 años. ¿Cuántos años tiene uno de los quintillizos de Liliana?
Problema 120:
Andrea dice: “Dentro de 20 años tendré 4 veces la edad que tenía hace 10 años. ¿Qué edad tiene Andrea?
Problema 119:
Dentro de ocho años la edad de Pedro será la que tiene Juan ahora. Dentro de 15 años Pedro tendrá 4/5 de la edad que entonces tendrá Juan. ¿Cuál era la suma de las edades de Juan y Pedro cuando Juan tenía el doble de la edad de Pedro?
Problema 118:
Pedro y Manuel conversan acerca de sus edades, Pedro dice: “Dentro de 10 años mi edad será el doble de la tuya”, Manuel responde: Hace cinco años tu edad era cinco veces la mía”. ¿Cuáles son sus edades actuales? Dar por respuesta la suma de las edades.
Problema 117:
Si la edad que tuviste hace 10 años más la edad que tienes y la edad que tendrás dentro de 8 años suman 118, ¿cuál será tu edad dentro de 13 años?
Problema 116:
Si la edad de Francisco es mayor en 13 años que el triple de la edad que tuvo hace 53 años, ¿cuál es su edad actual?
Problema 115:
Mi edad y tu edad suman 40 años, dentro de 10 años mi edad será un número capicúa y tu edad una de las cifras de dicha capicúa elevado al cubo. ¿Cuál fue mi edad hace 5 años?
Problema 114:
En 1988 la edad de Mariana fue el doble de la de Marco y en 1980 era el cuádruple. ¿Cuál será la edad de Mariana en 1998?
Problema 113:
Juan Carlos compra su primer coche cuando tiene 27 años y cuando tiene 38 años compra un segundo coche. ¿Cuál será su edad cuando la suma de los años de los coches sea de 29 años?
Problema 112:
La edad de Ana es el doble de la de Inés. Si hace 12 años la relación de sus edades era 1/8, ¿qué edad tendrá Ana dentro de 7 años?
Problema 111:
Mi edad actual es la mitad de la que tú tendrás cuando yo tenga el triple de la edad que tú tienes. Si hace 10 años nuestras edades sumaban 8, ¿cuál es tu edad actual?
Problema 110:
La edad de Sergio es 1/3 de los 2/5 de la edad de Daniel. Si dentro de 8 años la suma de sus edades es 67 años, ¿cuál será la edad de Sergio dentro de 18 años?
Problema 109:
El señor Eduardo tuvo un hijo a los 32 años y un nieto a los 18 años más tarde, actualmente el nieto tiene 22 años, y el abuelo afirma tener 60 años y el hijo 38 años. Halle el producto de los años que ocultan ambos.
Problema 108:
Hace 10 años una madre tenía 10 veces la edad de su hija. Si actualmente la suma de la edad de la madre con el doble de la edad de la hija es iguala 66 años, ¿cuál es la diferencia de sus edades?
Problema 107:
La edad actual de Luis y la de Nino son entre sí como 9 es 8. Cuando Nino tenga la edad que ahora tiene Luis, éste tendrá el doble de la edad que tenía Nino hace 18 años. Halle la diferencia de sus edades.
Problema 106:
Rommel le dice a Sebastián: “yo tengo el doble de la edad que tú tenías, cuando yo tenía la edad que tú tienes y cuando tú tengas mi edad, la suma de nuestras edades será 63 años”. ¿Cuántos años tiene Sebastián?
Problema 105:
Él tiene la edad que ella tenía, cuando él tenía la tercera parte de la edad que ella tiene. Si ella tiene 16 años más que él, ¿cuántos años tiene ella?
Problema 104:
Yo tengo el doble de tu edad, pero él tiene el triple de la mía. Si dentro de 6 años él va a tener el cuádruple de tu edad, ¿dentro cuántos años tendré 30 años?
Problema 103:
Cuando tenías 10 años yo tenía la mitad de la edad que tú tendrás cuando yo tenga el doble de la edad que tienes. Si nuestras edades suman 28 años, ¿qué edad tengo?
Problema 102:
Las dos terceras partes de la edad de Alfredo exceden en 6 años a la edad de Berta, y hace 6 años la edad de Berta era los dos novenos de la de Alfredo. ¿Qué edad tiene Alfredo?
Problema 101:
Antonio quería conocer la edad de su profesor, y éste le respondió diciendo: “Si a mi edad le multiplicas por 2, al resultado lo divides por 18, luego lo elevas al cubo, finalmente, le sumas 13, obtendrás como resultado 21 años.” ¿Hace cuántos años nació el profesor?
Problema 100:
Me preguntaron por la edad que tengo y respondí: ”Si a 10 veces los años que tendré dentro de 10 años le restas 10 veces los años que tenía hace 10 años, resulta 9 veces más los años que tengo”. ¿Cuál es mi edad actual?
Problema 99:
La suma de las edades de un padre y de sus dos hijos es 48. Dentro de diez años el doble de la suma de las edades de los hijos excederá en 6 años a la edad del padre. Cuando nació el pequeño, la edad del padre excedía 26 unidades al triple de la edad que tenía el hijo mayor. Calcula la edad de los tres.
Problema 98:
¿Cuántos años tiene una persona, sabiendo que la raíz cuadrada de la edad que tenía hace 4 años más la raíz cuadrada de la edad que tendrá dentro de 9 años suma 13?
Problema 97:
Si 3 veces la edad de mi hermano es 2 veces mi edad y hace 3 años, 3 veces su edad era la mía. ¿Cuántos años tengo?
Problema 96:
Álex le dice a Betty, cuando yo nací, tenías 6 años. Cuando César nació yo tenía la tercera parte de lo que tú tenías cuando yo nací, pero cuando nació David, César tenía el doble de lo que yo tenía cuando César nació, pero cuando David tenga un año menos de lo que yo tenía cuando David nació, ¿qué edad tendrá César en ese momento?
Problema 95:
Cuando tengas mi edad, yo tendré la que tú tendrás cuando yo tenga 35 años. Si cuando naciste yo tenía 10 años. ¿Qué edad tengo?
Problema 94:
Nuestras edades suman 47 años; sin embargo, cuando tenías 15 años yo tenía la edad que tendrás dentro de 2 años. ¿Qué edad tienes?
Problema 93:
Dentro de 4 años la edad de Isabel será un cuadrado perfecto, pero hace 3 años era el cuadrado perfecto anterior al inicial. ¿Cuál era su edad hace 6 años?
Problema 92:
Pablo y su abuelo tenían en 1928 tantos años como indicaban las dos últimas cifras de su año de nacimiento. Entonces cuando nació Pablo la edad del abuelo era:
Problema 91:
Una persona tiene en 1988 tantos años como el producto de las dos últimas cifras del año de su nacimiento. Entonces la edad actual (2014), considerando que este año ya celebró su onomástica, es:
Problema 90:
Betsy nació en 19ab y en 1990 tuvo (a+b) años. Entonces el año que llego a tener (2a+b) años fue:
Problema 89:
La suma de las edades de una pareja de esposos, cuando nació su primer hijo, era la mitad de la suma de sus edades actuales. Si actualmente el hijo ha cumplido 25 años. ¿Qué edad tenía el hijo cuando las edades de los tres sumaban 95 años?
Problema 88:
Rosa le dice a Isabel: “La razón de nuestras edades es ¾; además yo tengo la edad que tú tenías, cuando mi padre tenía la edad de tu padre. Cuando tu padre tenga la edad de mi padre, mi edad será la mitad de la edad que tu padre tenía hace 10 años y tu edad será la mitad de la edad que tenía mi padre hace 5 años”. Entonces la suma de las edades de Rosa e Isabel, es:
Problema 87:
Magaly le dice a Gisela: Mi edad hace muchos años era mayor de 20 pero menor de 30; y dicho años se podía calcular de la siguiente manera: sumando los cuadrados de cada una de los dos primeras cifras y restándole la suma de cada uno de los cuadrados de las dos últimas cifras de aquel año. ¿Cuántos años tiene actualmente (2004) sabiendo que es el mayor posible?
Problema 86:
Al ser preguntado Eduardo por la edad de su hermana, respondió: “Cuando yo tenía 14 años, mi hermana tenía la mitad de la edad que tenía mi padre; actualmente sucede lo mismo con mi edad y la edad de mi padre; en cambio hace 16 años, mi edad era la mitad de la edad que tenía mi hermana”. Entonces la edad de la hermana de Eduardo es:
Problema 85:
Diana le dice a Carlos: “Mi edad es 4 años menos que la edad que tú tenías cuando yo tenía 8 años menos de la edad que tú tienes, y cuando tú tengas el doble de la edad que yo tengo, nuestras edades sumarán 82 años. ¿Qué edad tiene Diana?
Problema 84:
Piero le dice a Juana: “Yo tengo el doble de la edad que tú tenías cuando Luis tenía la mitad de la edad que tienes; y cuando Luis tenga la edad que tengo, yo tendré el triple de la edad que él tenía cuando yo te dije, y tú tendrás el doble de la edad que tenías hace 7 años. Halle la edad de Piero.
Problema 83:
La edad de Antonio es el doble de la que tenía Víctor cuando Antonio tenía la edad actual de Carlos; si en aquel entonces Carlos tenía 3 años menos que la séptima parte de la edad actual de Víctor, y actualmente sus edades suman 90 años, ¿cuántos años tiene Antonio?
Problema 82:
Juan le dice a José: cuando tú tenías 7 años menos de la edad que yo tengo, yo tenía 3 años menos de la edad que tú tienes y cuando tenga el doble de la edad que tú tienes, nuestras edades sumarán 66 años. La edad de José es:
Problema 81:
Luis le dice a Clara: “tengo el triple de la edad que tú tenías cuando yo tenía la mitad de la edad que tú tienes, y cuando tengas la edad que yo tengo, yo tendré el doble de la edad que tú tenías hace18 años”. Entonces la suma de las edades de Luis Clara es:
Problema 80:
José le dice a Pablo: “Yo tengo el doble de la edad que tú tenías cuando yo tenía la edad que tú tienes; pero cuando tú tengas la edad que yo tengo, la suma de nuestras edades será 63 años. Entonces la suma de nuestras edades actuales es:
Problema 79:
La edad de José es los 3/2 de la edad de Luis. Si José hubiera nacido 10 años antes y Luis 5 años después, entonces la razón de ambas edades sería 16/5 de la razón existente si José hubiese nacido 5 años después y Luis 10 años antes. ¿Qué edad tuvo uno de ellos cuando el otro nació?
Problema 78:
Si la relación de las edades de Popeye y Olivia es de 2 a 3; y la de Olivia y Pluto es de 6 a 5; si hace 4 años la edad que tenía Pluto era igual a la edad que tiene Popeye, y dentro de “n” años la edad de Olivia será la suma de las edades que tenía Popeye y Olivia hace 4 años. Halle la edad de Pluto dentro de “n” años.
Problema 77:
La suma de las edades de una pareja de esposos, cuando nació su primer hijo, era la mitad de las sumas de sus edades actuales. Si actualmente el hijo ha cumplido 25 años, ¿Qué edad tenía el hijo cuando las edades de los tres sumaban 95 años?
Problema 76:
Yo tengo el triple de la edad que tú tenías cuando yo tenía la edad que tú tienes. Pero cuando tú tengas la edad que yo tengo nuestras edades sumarán 105 años
Problema 75:
Luis le dice a Miguel “Tengo el triple de la edad que tú tenías, cuando yo tenía la edad que tú tienes; pero cuando tú tengas la edad que yo tengo, la suma de nuestras edades será 56 años. ¿Cuántos tiene Luis?
Problema 74:
Mario nació en el año 19ba y en el año 19ab tenía (a+ b) años. ¿En qué año tuvo a por b años?
Problema 73:
Un padre decía a su hijo: “Hoy tu edad es 1/3 de la mía y dentro de 13 años será justamente ½. ¿Qué edad tenemos cada uno?
Problema 72:
Roberto tiene 24 años; su edad es el séxtuplo de la edad que tenía Betty cuando Roberto tenía la tercera parte de la edad que tiene Betty. ¿Cuál es la edad de Betty?
Problema 71:
José le dice a Miriam; “si al triple de mi edad se le quita 16 años, tendría lo que me falta para tener 88 años”. Elena le responde: “si al triple de la edad que tendré dentro de 4 años le sumo el cuádruple de la edad que tenía hace 9 años, resultará el séxtuplo de mi edad”. ¿Cuál es la suma de nuestras edades?
Problema 70:
Se sabe que la edad de un padre y la de su hijo, hace 8 años la edad del primero fue el cuádruple de la del segundo; dentro de 12 años solo será el doble de la de su hijo. ¿Cuál es la diferencia de edad?
Problema 69:
Las edades de tres hermanos hace 2 años estaban en la misma relación que 3, 4 y 5. Si dentro de dos años serán como 5, 6 y 7. ¿Cuál es la edad del mayor?
Problema 68:
Hace “m” años Isabel, tenía 28 años, dentro de 3m años tendrá 44 años. ¿Cuál es la edad actual de Isabel?
Problema 67:
Dentro de 20 años, la edad de María será a la de Diana como 4 es a 3; si hace 13 años la edad de María era el quíntuplo de la edad de Diana, ¿cuál es la edad de ambas?
Problema 66:
Las edades de Alberto y Mirito suman en la actualidad 120 años. Si Alberto tiene la edad que ella tenía cuando él tenía la tercera parte de su edad actual. ¿Cuál es la edad de Mirito?
Problema 65:
Julio le dice a Diana: “yo tengo el triple de la edad que tenías cuando yo tenía la edad que tú tienes y cuando tú tengas la edad que yo tengo la diferencia de nuestras edades será 12 años. ¿qué edad tiene Diana?
Problema 64:
Cuando yo tenía 20 años, tú tenías la tercera parte de la edad que tienes. Si nuestras edades suman 95 años, ¿cuántos años tengo?
Problema 63:
Hace 12 años las edades de Alberto y Luis estaban en la relación de 4 a 3; en la actualidad sus edades suman 73. Entonces, ¿cuántos años deben pasar para que la relación sea de 8 a 7?
Problema 62:
Hace 8 años tenía la cuarta parte de años que tendré dentro de 16 años. Entonces, ¿dentro de cuántos años tendré el cuádruplo de los años que tenía hace 6 años?
Problema 61:
Él le dice a ella: “Yo tengo el triple de edad que tú tenías cuando yo tenía la edad que tú tienes”. Entonces la edad de ambos será, si sus edades suman 50 años.
Problema 60:
Pedro le dijo a Juan:” Yo tengo el doble de la edad que tú tenías cuando yo tenía la edad que tú tienes y cuando tú tengas la edad que yo tengo, la suma de nuestras edades será 63 años”. Hallar la edad de Pedro.
Problema 59:
La suma de las edades de A y B es de 84 años, y B tiene 8 años menos que A. Hallar ambas edades.
Problema 58:
La edad de A es el doble de la B y hace 15 años la edad de A era el triplo de la de B. Hallar las edades actuales
Problema 57:
La edad de Enrique es la mitad de la de Pedro; la de Juan el triplo de la de Enrique y la de Eugenio el doble de la de Juan. Si las 4 edades suman 132 años, ¿Qué edad tiene cada uno?
Problema 56:
Preguntado un hombre por su edad, contesta: si al doble de mi edad se le quitan 20 años se obtiene lo que me falta para llegar a 100. ¿Cuál es la edad de dicha persona?
Problema 55:
Un señor tiene 39 años y su hijo 9. ¿Dentro de cuántos años la edad del padre será el triple que la del hijo?
Problema 54:
Un padre tiene 35 años y su hijo 15. ¿Cuántos años hace que la edad del padre era el triple que la edad del hijo?
Problema 53:
Él tiene la edad que ella tenía cuando él tenía la tercera parte de la edad que ella tiene. Si ella tiene 8 años más que él. ¿Cuántos años tiene ella?
Problema 52:
Hállese la edad de una persona, sabiendo que si se añade 7 a la cuarta parte de su edad es lo mismo que si se le quita 3 a los 2/3 de su edad.
Problema 51:
Sabemos que mi tío tiene 27 años más que su hijo y que dentro de 12 años le doblará la edad. ¿Cuántos años tiene cada uno?
Problema 50:
La madre de Ana tiene el triple que ella, y dentro de 10 años solo tendrá el doble de la que entonces tenga su hija. ¿Qué edad tiene cada una?
Problema 49:
Un bisabuelo le dijo a su bisnieta. “Hoy tu edad es 1/5 de la mía y hace 7 años no era más que 1/7” ¿Qué edad tiene el bisabuelo y la bisnieta?
Problema 48:
La suma de las edades de tres personas es de 112 años. La mediana tiene 8 años más que la joven, y la mayor tiene tantos años como las otras dos juntas. ¿Qué edad tiene cada una?
Problema 47:
Yo tengo el triple de la edad que tú tenías cuando yo tenía la edad que tú tienes. Cuando tú tengas mi edad actual, entre los dos tendremos 112 años. ¿Qué edad tengo?
Problema 46:
María dice: dentro de 16 años mi edad será tres veces la que tenía hace dos años. ¿Qué edad tengo?
Problema 45:
Hace 4 años, Rosa tenía 20 años. ¿Cuántos tendrá dentro de 6 años?
Problema 44:
Las edades de Víctor y Marabel son como 3 es a 2, si hace 4 años estaban en relación de 5 a 3. ¿Dentro de cuántos años estarán en relación de 4 a 3?
Problema 43:
Hace 10 años la edad de un hijo era un séptimo de la de su madre, y dentro de 10 años la edad de la madre será el doble de la de su hijo. Hallar las edades actuales de ambos.
Problema 42:
¿La relación entre las edades de dos niños de 10 y 14 años?
Problema 41:
Ernesto tiene 5 años más que Rocío. Si la suma de sus edades es 21, ¿cuántos años tiene Rocío?
Problema 40:
Mi edad y la edad de mi tío suman 36 ¿Qué edad tengo si mi tío tiene el doble de mi edad?
Problema 39:
Hace dos años tu edad era mayor que la de María por 8 años. Si actualmente tu edad es el triple de la María . ¿Qué edad tendrá el próximo año?
Problema 38:
Mi tío tiene 30 años más que yo, pero dentro de 20 tendrá el doble. ¿Qué edad tenemos cada uno?
Problema 37:
La suma de las edades de un padre y su hijo es 35 años. Si dentro de 20 años la edad del padre será dos veces la de su hijo ¿Qué edad tiene el hijo ahora?
Problema 36:
Camilo tiene 7 años y su padre 49. Si Juan guarda con su padre la misma proporción que Camilo y su padre; y el padre de Juan tiene 25 años . ¿Cuántos años tiene Juan?
Problema 35:
La edad de «a» excede al doble de la edad de «b» en 10. Si «a» tiene 60 años hallar la diferencia de sus edades.
Problema 34:
Las dos terceras partes de la edad de A excede en 4 años a la de B, y, hace 8 años, la edad de A era doble que la de B. ¿Cuál es la edad de cada uno de ellos?
Problema 33:
La edad de Juan era hace 9 años la raíz cuadrada de la que tendrá dentro de 11. Determina la edad actual.
Problema 32:
Al preguntarle a Maribel sobre su edad, ella responde: si a la edad que tengo le resto los 2/3 tendría la mitad disminuida en dos años. ¿Qué edad tiene?
Problema 31:
Laura tiene el doble de años que su hijo. Hace 10 años la suma de las edades era 46. ¿Cuál es la edad de su hijo?
Problema 30:
Averiguar las edades que tienen cuatro individuos, sabiendo: que forman una progresión aritmética creciente; que sumada la edad del primero con la del cuarto, da 71; y que multiplicando ambas edades, resulta 1078.
Problema 29:
Hace dos años la edad de un padre era 11 veces la del hijo y dentro de un año la edad del padre será el cuadrado de la del hijo. Hallar las edades actuales de los dos.
Problema 28:
La edad de un niño será dentro de tres años un cuadrado perfecto, y hace tres años que su edad era precisamente la raíz de este mismo cuadrado. ¿Qué edad tiene?
Problema 27:
Un padre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad del padre sea el doble que la del hijo?
Problema 26:
¿Qué edad tengo ahora si dentro de 12 años tendré el triple de la edad que tenía hace 6 años?
Problema 25:
Miguel tiene 4 años más que su primo Ignacio y, dentro de 3 años, entre los dos sumarán 20 años. ¿cuántos años tiene cada uno?
Problema 24:
Hace 4 años las edades de dos personas están en relación de 2 a 3; y dentro de 4 años estarán en la relación de 4 es a 5. ¿Qué edad tienen dichas personas?
Problema 23:
La edad de una persona es el doble de la otra; hace siete años, la suma de las edades era igual a la edad actual de la mayor. ¿Cuál es la edad de ambas personas?
Problema 22:
Un padre tiene 46 años y su hijo 12. ¿Cuándo la edad del padre será justamente el triple de la edad del hijo?
Problema 21:
Un padre tiene seis veces la edad de su hijo, y la suma de las dos edades es 91. ¿Cuántos años tiene cada uno de ellos?
Problema 20:
Hace 18 años, la edad de una persona era el doble de la de otra; dentro de 9 años la edad de la primera no será ya más que los 5/4 de la segunda. ¿Cuál es su edad actual?
Problema 19:
La raíz cuadrada de la edad del padre nos da la edad del hijo, y dentro de 24 años la edad del padre será el doble que la del hijo. Halla las edades.
Problema 18:
Un padre decía a su hijo: Ahora tu edad es el quinto de la mía; hace 5 años no era más que el noveno; ¿ qué edad tenemos los dos?
Problema 17:
La edad de una persona es doble de la de otra, y hace 7 años la suma de las edades de las dos personas era igual a la edad actual de la primera; ¿cuáles actualmente las edades de las dos personas?
Problema 16:
Un padre tiene 40 años y su hijo 12, ¿cuántos años hace que la edad del padre era 5 veces la del hijo?
Problema 15:
Dentro de 11 años, la edad de Pedro será la mitad del cuadrado de la que tenía hace 13 años. Calcula la edad de Pedro.
Problema 14:
Un padre tiene 27 años, su hijo 3; ¿dentro de cuántos años la edad del hijo será el cuarto de la del padre?
Problema 13:
La suma de las edades de tres personas es de 100 años. Búsquese la edad de cada una, sabiendo que la de en medio tiene 10 años más que la más joven y que la mayor tiene tantos años como las otra dos juntas.
Problema 12:
La edad de un padre es hoy 3 veces la de su hijo, y hace 6 años era 5 veces la edad del mismo. ¿Cuántos años tiene cada uno?
Problema 11:
Un padre tiene 30 años más que su hijo, y dentro de 5 años la edad del padre será triple de la de hijo. ¿Qué edad tiene cada uno?
Problema 10:
Un hijo dice a su padre: «Hoy tu edad es el triple de la mía, y dentro de 12 años será únicamente el doble». ¿Qué edad tiene cada uno?
Problema 9:
Víctor tiene tres años más que su hermano, y dentro de 4 años la suma de sus edades será 33 años. ¿Qué edad tiene cada uno?
Problema 8:
La madre de Luis tiene triple edad que él, y dentro de 14 años solo tendrá el doble de la que entonces tenga éste. ¿Qué edad tiene cada uno?
Problema 7:
José tiene 10 años más que su hermana, y dentro de 6 años tendrá el doble edad que la que entonces tenga ésta. ¿Qué edad tiene cada uno?
Problema 6:
Juan tiene 4 años más que su hermana, y hace 6 años tenía el doble edad que la que entonces tenía su hermana. ¿Cuántos años tiene actualmente cada uno?
Problema 5:
Un señor tiene dos hijos, de los cuales uno tiene 6 años más que el otro. Después de dos años, la edad del padre será doble de la suma de las edades de sus hijos, y hace 6 años su edad era 4 veces la suma de las edades de sus hijos. ¿ Cuál es la edad de cada uno?
Problema 4:
Las edades de una madre y de sus dos hijos suman 60 años. Búsquese la edad de cada uno de los hijos, sabiendo que el mayor tiene tres veces la edad de su hermano y que la madre tiene el doble de edad de sus hijos.
Problema 3:
Restando del cuadrado de la edad de una persona el producto de esta misma edad por 15, se halla 16 de diferencia. Calcular esta edad.
Problema 2:
La edad de un niño será dentro de tres años un cuadrado perfecto, y hace tres años que su edad era precisamente la raíz cuadrada de este mismo cuadrado. ¿ Qué edad tiene?
Problema 1:
La edad actual de un padre es el triple que la de su hijo y dentro de 14 años será el doble. ¿Qué edad tiene cada uno?
