Problema 135:
Dada la expresión:

Calcula el valor de x para que el valor de y sea igual a a.
Problema 134:
Hallar la fracción generatriz de:

Problema 133:
¿Es divisible…

Justifica la respuesta.
Problema 132:
Simplifica la fracción:

Obsérvese el valor que toma para x= 2; y x= 3.
Problema 131:
Escribe una ecuación de segundo grado cuyas raíces sean 5 y -4
¿Cómo se obtiene?
Problema 130:
Resolver:

Problema 129:
Resolver:

Problema 128:
Hallar el verdadero valor de la fracción

Para x= -2
Problema 127:
Resolver la ecuación
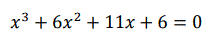
Sabiendo que sus soluciones son números enteros.
Problema 126:
El cociente
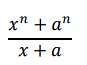
¿Es siempre exacto? En caso negativo, di cuándo y por qué lo es.
Problema 125:
Determinar los coeficientes del polinomio
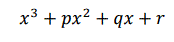
Sabiendo: 1º, que se anula para x= 1; 2º, que toma el valor 9 para x= 2, y 3º, que toma el valor 40 para x= 3.
Problema 124:
Hallar la fracción generatriz:

Problema 123:
Simplificar:

Problema 122:
Descomponer en suma de fracciones simples la fracción algebraica:

En la que n es el número de divisores de 54.000.
Problema 121:
Hallar el máximo común divisor (m.c.d.) de los polinomios:

Siendo:

Los tres primeros cocientes incompletos del desarrollo en fracción continua de la fracción:

Problema 120:
Determinar las cifras x e y a fin de que el número 2x45y sea múltiplo de 72.
Problema 119:
Las tres raíces de la ecuación:

Son números enteros. Se pide:
- Hallar las tres raíces, x1, x2 y x3
- Una vez obtenidas dichas raíces, descomponer la fracción

En la suma de tres fracciones,

Es decir, hallar A, B y C con la condición que

Problema 118:
Dados los polinomios:

Determinar el valor de a, sabiendo que el máximo común denominador de ambos es un polinomio de segundo grado. Encontrado este, resolver las ecuaciones A(x)= 0 y B(x)= 0.
Problema 117:
Sea la identidad:

Calcular A, B, C y D
Problema 116:
Reconocer que la ecuación:

Admite la raíz x= -1
Rebajar de grado dicha ecuación y determinar las otras dos raíces de la misma.
Problema 115:
Resolver la ecuación:

Y hallar la suma de los cuadrados de las raíces negativas.
Problema 114:
Si se verifica que:

Simplificar:

Problema 113:
Calcular el valor de x, en:

Problema 112:
Calcular el valor de x, en:

Problema 111:
Hallar el resultado de la expresión:

Problema 110:
Resolver la expresión:

Problema 109:
Resolver la expresión:

Problema 108:
Simplificar la expresión:

Problema 107:
Simplificar la expresión:

Problema 106:
Resolver:
Problema 105:
Racionalizar el denominador y simplificar la expresión:
Problema 104:
Ordena de menor a mayor las siguientes potencias:
Problema 103:
¿Cuántos cuadrados perfectos hay menores que 40.000? Justifica tu respuesta
Problema 102:
¿Cómo podrías averigua, sin efectuar la división, si el polinomio, 2x3-3x-1 es divisible por x+1? Justifica la respuesta
Problema 101:
¿Qué volumen ocupa un quintal métrico de agua? Expresa este volumen en m3 y en cm3.
Problema 100:
Halla el peso, expresado en kilogramos, de 7m3 43 dm3 58 cm3 de agua. Explica la respuesta.
Problema 99:
El cociente exacto de una división es 6. Si multiplicamos el dividendo por 8 y el divisor por 2, ¿cuál será el nuevo cociente?
Problema 98:
¿Qué es una hectárea? ¿Cuántos dm2 tiene? Expresar en hectáreas la medida de 570m2
Problema 97:
En un cierto problema el valor de la solución es:
Simplifica la expresión, y después efectúa el cálculo.
Problema 96:
Calcular el ángulo x sabiendo que 4x-72º 36´= 67º 25´-x. ¿Cuánto mide el ángulo complementario de x?:
Problema 95:
Simplificar la expresión:
Y una vez simplificada calcula su valor aproximado hasta la centésima.
Problema 94:
Dada la expresión:
Se pide:
- Sustituye x por
 y racionaliza la expresión que resulte.
y racionaliza la expresión que resulte. - Calcula su valor aproximado hasta la centésima.
Problema 93:
Si la milla marina es la 60ª parte de un grado de meridiano terrestre y el nudo marino es la centésima vigésima (1/120) parte de la milla marina, ¿cuántos metros tiene la milla y el nudo marino?
Problema 92:
Simplificar la expresión: C= AB, siendo:
Hallar el valor numérico de C para A= -2
Problema 91:
Reducir la siguiente fracción a su más simple expresión:
Problema 90:
Ordena de menor a mayor los números:
2-2; 20; 23; 2-1; 2+1; 24
Problema 89:
Comprueba la siguiente igualdad, indicando si es una ecuación o una identidad.
Problema 88:
Simplifica la expresión razonando la solución.
Problema 87:
Convertir en centilitros y después en centímetros cúbicos 3 dm3; ¼ de litro; 3,2 Dl; 2,25 dl.
Problema 86:
Dada la siguiente expresión, escribirla en forma de producto de dos factores
Problema 85:
¿Se puede simplificar la siguiente expresión?
Razona la respuesta.
Problema 84:
¿Cuál es el menor número por el hay que multiplicar a 120 para obtener otro número que sea cuadrado perfecto?
Razona la respuesta.
Problema 83:
¿Es cierta la siguiente igualdad?
Razona la respuesta.
Problema 82:
Racionalizar el denominador de la siguiente fracción:
Problema 81:
Transforma la expresión siguiente en suma de radicales simples
Problema 80:
Calcular
Problema 79:
Simplificar:
Problema 78:
Deducir cuál de las dos expresiones siguientes adquiere mayor valor numérico: para a=3 y b=2
Problema 77:
Simplificar:
Problema 76:
Simplificar:
Problema 75:
Simplificar:
Problema 74:
Simplificar
Problema 73:
Simplificar
Problema 72:
Hallar P(x) sabiendo que
Problema 71:
Dado los polinomios
a) Hallar su m.c.d.
b) Hallar su m.c.m
Problema 70:
Hallar A y B para que la ecuación sea indeterminada
Problema 69:
Resolver:
Problema 68:
Calcular el m.c.m. de los polinomios
Problema 67:
Calcular el m.c.d. de los polinomios:
Problema 66:
Hallar el valor de la siguiente expresión:
Problema 65:
Razona si son ciertas o falsas las identidades siguientes:
Problema 64:
Resolver:
Problema 63:
Hallar la solución entera y positiva de la ecuación:
Problema 62:
Transforma la expresión siguiente en suma de radicales simples:
Problema 61:
Resolver:
Problema 60:
Transforma la expresión siguiente en suma de radicales simples
Problema 59:
Transforma la expresión siguiente en suma de radicales simples
Problema 58:
Hacer racional el denominador de las siguientes fracciones:
Problema 57:
Hacer racional el denominador de las siguientes fracciones:
Problema 56:
Hacer racional el denominador de las siguientes fracciones:
Problema 55:
Hacer racional el denominador de las siguientes fracciones:
Problema 54:
Hacer racional el denominador de las siguientes fracciones:
Problema 53:
Hacer racional el denominador de las siguientes fracciones:
Problema 52:
Hacer racional el denominador de las siguientes fracciones:
Problema 51:
Problema 50:
Hacer racional el denominador de las siguientes fracciones:
Problema 49:
Transforma la siguiente expresión en suma de dos radicales sencillos:
Problema 48:
Hacer racional el denominador de la siguiente fracción:
Problema 47:
De las dos raíces,
, ¿cuál es la mayor?
Problema 46:
Transforma la expresión siguiente en suma de radicales simples:
Problema 45:
Efectuar las operaciones siguientes:
Problema 44:
Hacer racionales los denominadores de la fracción:
Problema 43:
Transforma las siguientes fracciones
en otras equivalentes que tengan el mismo numerador
Problema 42:
¿Cómo racionalizas el denominador en la expresión siguiente:
Problema 41:
Racionaliza el denominador de la fracción:
Problema 40:
Racionalizar el denominador de:
Problema 39:
Hacer irreducible la fracción:
Problema 38:
¿Cuál es el verdadero valor de la fracción
Problema 37:
Resolver:
Problema 36:
Efectuar las operaciones siguientes:
Problema 35:
Efectuar las operaciones siguientes:
Problema 34:
Efectuar las operaciones siguientes:
Problema 33:
Resolver:
Problema 32:
Resolver:
Problema 31:
Resolver
Problema 30:
Resolver
Problema 29:
Resolver
Problema 28:
Resolver
Problema 27:
Transforma y simplifica la expresión
hasta que resulte igual a «a»
Problema 26:
Transformar la expresión :

en producto de tres factores
Problema 25:
Transformar la expresión :
Problema 24:
Efectuar la siguiente división:
Problema 23:
Efectuar la siguiente división:
Problema 22:
Descomponer en dos factores las expresiones siguientes:
Problema 21:
Sacar factor común:
Problema 20:
Determinar m de tal manera que:
sea divisible por x-a
Problema 19:
Determinar m de tal manera que:
sea divisible por 2x+1
Problema 18:
Escribir los cocientes sin efectuar las operaciones:
Problema 17:
Escribir los cocientes sin efectuar las operaciones:
Problema 16:
Simplificar la expresión:
Problema 15:
Calcular
Problema 14:
Resolver
Problema 13:
Hallar el verdadero valor de
Problema 12:
Calcular
Problema 11:
Para que el polinomio
sea divisible por x-2, ¿qué valor se debe dar a m?
Problema 10:
Hallar el verdadero valor de la siguiente fracción para x=5
Problema 9:
Hallar el verdadero valor de la siguiente fracción para x=a
Problema 8:
Racionaliza el denominador de la siguiente expresión
Problema 7:
La suma
Justifica la respuesta.
Problema 6:
Despeja t en la siguiente igualdad:
Problema 5:
Halla el binomio cuyo cuadrado sea
Razónalo
Problema 4:
¿Cuál es la expresión conjugada de
¿Qué propiedad tiene el producto de dos expresiones conjugadas?
Problema 3:
¿Cómo se descompone el polinomio
en producto de tres factores del primer grado?
Aprovechando dicha descomposición, resuelve la ecuación
Problema 2:
¿Es exacta la división de
Calcula el cociente y el resto
Problema 1:
Para que el polinomio
sea divisible por x+2, ¿cómo determinas el valor de m?. Razónalo






















































































