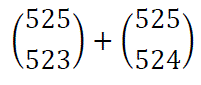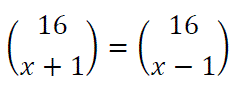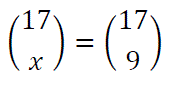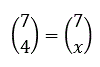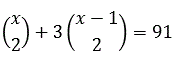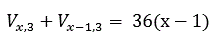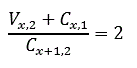Problema 96:
Cuánto tiene que valer x en la expresión:
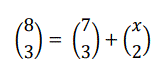
Y escribir la propiedad general.
SOLUCIÓN PROBLEMA COMBINATORIA 96
Problema 95:
Hallar el valor de A+B, sabiendo que A es la solución posible de la ecuación:
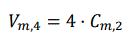
y B la suma de los cinco primeros términos de la progresión:
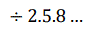
SOLUCIÓN PROBLEMA COMBINATORIA 95
Problema 94:
Calcular:
a.- El número n de números de cinco cifras que se pueden escribir, empleando únicamente las cifras impares, sin repetir en cada número ninguna cifra.
b.- La suma de los números así formados.
c.- El valor de la derivada de la función

Para x= p en donde n es el número hallado en “a” y
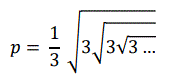
SOLUCIÓN PROBLEMA COMBINATORIA 94
Problema 93:
Resolver la ecuación:
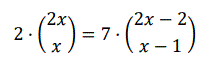
Supuesto que x es un número natural.
SOLUCIÓN PROBLEMA COMBINATORIA 93
Problema 92:
Con las cifras 1, 3, 4, 5 y 7 se pueden formar números de 5 cifras que no tengan ninguna repetida; se pide:
a.- Número total de números que se pueden formar.
b.- Número de ellos que son múltiplos de 4 y los que son múltiplos de 2.
c.- Número de ellos que son múltiplos de 11
d.- Escribir el menor y el mayor de los múltiplos de 11.
SOLUCIÓN PROBLEMA COMBINATORIA 92
Problema 91:
Resolver la ecuación:
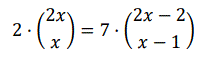
Supuesto que x es un número natural.
SOLUCION PROBLEMA COMBINATORIA 91
Problema 90:
El séxtuplo del número de combinaciones que se pueden formar con m objetos tomados de 3 en 3, es igual al número de variaciones que se pueden formar con m-1 objetos tomados de 4 en 4. Deducir el valor de m.
SOLUCIÓN PROBLEMA COMBINATORIA 90
Problema 89:
Con las diez cifras del sistema de numeración decimal, ¿cuántos números de 3 cifras diferentes se pueden formar? ¿Cuántos de ellos son múltiplos de 5?
SOLUCIÓN PROBLEMA COMBINATORIA 89
Problema 88:
Se tienen 7 libros grandes distintos, 5 medianos y 3 pequeños, ¿de cuántas maneras diferentes se pueden alinear en un estante si han de colocarse juntos los del mismo tamaño?
SOLUCIÓN PROBLEMA COMBINATORIA 88
Problema 87:
Se suponen formadas todas las permutaciones posibles con las cifras 1, 2, 3, 4, 5 y 9 y se toma una al azar. ¿Cuál es la probabilidad de que el número por ella representado sea múltiplo de 12?
SOLUCIÓN PROBLEMA COMBINATORIA 87
Problema 86:
Resolver la siguiente ecuación:
SOLUCIÓN PROBLEMA COMBINATORIA 86
Problema 85:
Hallar los valores de x que satisfacen a:
SOLUCIÓN PROBLEMA COMBINATORIA 85
Problema 84:
Hallar cuantos números de cuatro cifras distintas se pueden escribir con las cifras 0, 1, 2, 3, 4, 5. ¿Cuántos de esos números son divisibles por 5? ¿Cuántos son menores de 3.000?
SOLUCIÓN PROBLEMA COMBINATORIA 84
Problema 83:
Con las cifras 1, 2, 3, 4, 5, ¿cuántos números de cuatro cifras distintas pueden formarse que sean múltiplos de 3? ¿Y cuántos que sean múltiplos de 4?
SOLUCIÓN PROBLEMA COMBINATORIA 83
Problema 82:
Calcula m para que se verifique:
SOLUCIÓN PROBLEMA COMBINATORIA 82
Problema 81:
Con las letras de la palabra Aurelio se forman todas las permutaciones. ¿Cuántas de ellas tienen las dos consonantes separadas?
SOLUCIÓN PROBLEMA COMBINATORIA 81
Problema 80:
Dados los números 1, 2, 3, 4, 5, 6, 7, se trata de calcular la cantidad de números de cuatro cifras que se pueden formar sin repetirse ninguna de ellas, que cumplan las siguientes características:
- Total de números posibles.
- Que empiecen en uno y acaben en siete.
- Que no contengan ni el cuatro ni el cinco.
- Que no contengan el dos ni el siete y si el seis.
- Que contengan el uno.
- Que comiencen en cuatro, acaben en tres y no contengan ni el cinco ni el siete.
- Que la segunda cifra sea cinco y la última par.
- Que la segunda cifra sea dos y la última uno.
- Que empiecen en cuatro y no contengan el uno ni el seis.
- Que el primero y el último sean impares y los del medio pares.
- Que empiecen en impar y terminen en par.
- Que el primero, segundo y cuarto sean impares y el tercero par.
- Que contengan un impar.
- Que tengan más pares que impares.
- Que sean múltiplos de dos.
- Que sean múltiplos de cinco.
- Que acaben en tres y tengan dos pares.
- Que no contengan el uno ni el cuatro y tengan algún par.
- Que contengan el cinco y el seis y dos impares.
- Que los dos centrales sean pares.
SOLUCIÓN PROBLEMA COMBINATORIA 80
Problema 79:
Con los dígitos {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}:
A.- ¿Cuántos números de tres cifras se pueden formar? sin y con repetición
B.- ¿Cuántos de estos son impares? sin y con repetición
C.- ¿Cuántos son pares? sin y con repetición
D.- ¿Cuántos son divisible por cinco? sin y con repetición
E.- ¿Cuántos hay mayores que seiscientos? sin repetición
SOLUCIÓN PROBLEMA COMBINATORIA 79
Problema 78:
La selección peruana de voleibol está conformada por 18 chicas. ¿De cuántas maneras se puede conformar un equipo de 6 si se sabe que 3 de ellas se niegan a jugar en el mismo equipo?
SOLUCIÓN PROBLEMA COMBINATORIA 78
Problema 77:
En una quiniela futbolística de catorce encuentros, ¿cuántas columnas distintas podrían rellenarse, considerando que todas ellas tiene que tener como variantes cinco equis y tres doses?
SOLUCION PROBLEMA COMBINATORIA 77
Problema 76:
¿Cuántos grupos de cinco letras pueden formarse con las letras a, b y c, con la condición de que en cada uno de ellos aparezcan las dos consonantes sin repetirse?
SOLUCIÓN PROBLEMA COMBINATORIA 76
Problema 75:
El sistema binario de numeración únicamente dispones de dos dígitos, el 0 y el 1. ¿Cuántas agrupaciones de seis dígitos pueden formarse, con la condición de que cada una de ellas contenga cuatro ceros y dos unos? ¿De estas agrupaciones, cuántas tienen todas sus cifras significativas?
SOLUCIÓN PROBLEMA COMBINATORIA 75
Problema 74:
Con las cifras: 0,1, 2, 3, 4, 5 se desea saber: a) ¿Cuántos números de 4 cifras distintas pueden hacerse? b) ¿Cuántos son impares?
SOLUCIÓN PROBLEMA COMBINATORIA 74
Problema 73:
A un señor le tocan 13 discos a elegir de un grupo de 25. De estos 25 hay 5 que le gustan. ¿Cuántas formas distintas de elegir tiene cogiendo los 5 preferidos?
SOLUCIÓN PROBLEMA COMBINATORIA 73
Problema 72:
¿De cuántas maneras podemos colocar 7 libros de distinto tamaño de manera que el más grande y el más pequeño estén siempre juntos?
SOLUCIÓN PROBLEMA COMBINATORIA 72
Problema 71:
Disponemos de 5 libros de matemáticas y tres de lengua. ¿De cuántas formas distintas se pueden ordenar si han de ir juntos los de la misma asignatura?
SOLUCIÓN PROBLEMA COMBINATORIA 71
Problema 70:
¿Cuántos números de 5 cifras distintas no contienen ni el 2, ni el 4, ni el 6 en el sistema decimal?
SOLUCIÓN PROBLEMA COMBINATORIA 70
Problema 69:
Al comenzar una reunión se han intercambiado 351 apretones de manos. Calcular cuántas personas han asistido a la misma, en el supuesto de que todas ellas se hayan saludado.
SOLUCIÓN PROBLEMA COMBINATORIA 69
Problema 68:
En una clase compuesta por treinta alumnos, se desea seleccionar una comisión constituida por cuatro de ellos. ¿Cuántas combinaciones distintas podrían formarse? ¿Cuál sería el número de comisiones posibles, en el supuesto de que un alumno concreto debiera, obligatoriamente, formar parte de la comisión?
SOLUCIÓN PROBLEMA COMBINATORIA 68
Problema 67:
¿Cuántas rectas determinan diez puntos coplanarios no alineados?
SOLUCIÓN PROBLEMA COMBINATORIA 67
Problema 66:
Calcular el número de subconjuntos que posee un conjunto de seis elementos.
SOLUCIÓN PROBLEMA COMBINATORIA 66
Problema 65:
Calcular el número de subconjuntos ternarios que posee un conjunto de diez elementos.
SOLUCIÓN PROBLEMA COMBINATORIA 65
Problema 64:
¿Cuántas palabras de cinco letras pueden formarse con tres vocales y dos consonantes distintas, con la condición de que en cada palabra no figuren dos consonantes ni tres vocales seguidas?
SOLUCIÓN PROBLEMA COMBINATORIA 64
Problema 63:
¿De cuántas maneras se pueden extraer 2 bolas rojas y tres verdes de una urna que contiene 15 bolas rojas y 12 verdes?
SOLUCIÓN PROBLEMA COMBINATORIA 63
Problema 62:
Dado el conjunto {1, 1, 1, 1, 1, 2, 3, 3, 3, 4, 4}, determinar el número de permutaciones que puede formarse con sus elementos.
SOLUCIÓN PROBLEMA COMBINATORIA 62
Problema 61:
¿Cuántos números de diez cifras significativas distintas existen en el sistema de numeración decimal?
SOLUCIÓN PROBLEMA COMBINATORIA 61
Problema 60:
Una guardería animal dispones de 8 jaulas consecutivas. ¿De cuántas maneras pueden situarse en las mismas cinco perros y tres gatos, de modo que un gato no se encuentre nunca entre dos perros?
SOLUCIÓN PROBLEMA COMBINATORIA 60
Problema 59:
¿Cuántas palabras de dos vocales y dos consonantes se pueden formar con cuatro consonantes y dos vocales, con la condición de que no han de figurar dos vocales seguidas?
SOLUCIÓN PROBLEMA COMBINATORIA 59
Problema 58:
Se tienen los números 5874 y 12369. ¿Cuántos números enteros y diferentes pueden formarse, que contengan dos cifras no repetidas del primero de aquéllos y tres no repetidas del segundo?
SOLUCIÓN PROBLEMA COMBINATORIA 58
Problema 57:
¿Cuántas permutaciones pueden formarse con las letras que entran en la palabra PERMUTACIÓN? ¿Cuántas que empiecen con la primera letra y cuántas que empiecen con las tres primeras en el orden en que están colocadas?
SOLUCIÓN PROBLEMA COMBINATORIA 57
Problema 56:
Calcular la suma de todos los números de cinco cifras significativas distintas, superiores que pueden formarse con los dígitos 0, 1, 2, 3, 4, 5 y 6.
SOLUCIÓN PROBLEMA COMBINATORIA 56
Problema 55:
¿Cuántos números de 6 cifras son capicúas? ¿Y de 5?
SOLUCIÓN PROBLEMA COMBINATORIA 55
Problema 54:
Calcular la suma de todos los números de cuatro cifras distintas, superiores a 3.000 que pueden formarse con los dígitos 1, 3, 5, 7 y 9.
SOLUCIÓN PROBLEMA COMBINATORIA 54
Problema 53:
1.- ¿Cuántos números de 6 cifras distintas se pueden obtener con las del conjunto {0, 1, 2, 3, 4, 5, 6}
2.- ¿Cuántos empiezan por número par?
3.- ¿Cuántos empiezan por número impar?
4.- ¿Cuántos terminan en 2?
5.- ¿Cuántos empiezan y terminan por cifra impar?
6.- ¿Cuántos empiezan y terminan por cifra par?
SOLUCIÓN PROBLEMA COMBINATORIA 53
Problema 52:
Calcular la suma de todos los números de tres cifras distintas que pueden formarse con los dígitos 2, 4, 6 y 8.
SOLUCIÓN PROBLEMA COMBINATORIA 52
Problema 51:
¿De cuántas maneras pueden sentarse siete personas en una mesa en la que las sillas están colocadas en línea recta? ¿Y si la mesa fuese redonda y las sillas estuvieran colocadas a su alrededor?
SOLUCIÓN PROBLEMA COMBINATORIA 51
Problema 50:
En una carrera participan ocho corredores. Calcular el número de boletos que sería preciso rellenar para tener la seguridad de acertar un pleno en una quiniela consistente en pronosticar el orden de llegada de todos los participantes.
SOLUCIÓN PROBLEMA COMBINATORIA 50
Problema 49:
Un club de fútbol dispone de dos porteros, cinco defensas, cuatro medios y seis delanteros. Calcular cuántos equipos distintos se podrían alinear considerando que un equipo de fútbol se compone de un portero, tres defensas, dos medios y cinco delanteros, y que cada jugador solamente se puede alinear en su propia demarcación.
SOLUCIÓN PROBLEMA COMBINATORIA 49
Problema 48:
Calcular cuántos números de cuatro cifras distintas, mayores que 5.400, se pueden formar con los dígitos 0,1, 2, 3, 4, 5 y 6.
SOLUCIÓN PROBLEMA COMBINATORIA 48
Problema 47:
¿Cuántas jugadas distintas pueden resultar de extraer cuatro cartas de una baraja de cuarenta, suponiendo que todas las cartas tienen el mismo valor?
SOLUCIÓN PROBLEMA COMBINATORIA 47
Problema 46:
Calcular el valor del mayor de todos los números combinatorios de numerador 14.
SOLUCIÓN PROBLEMA COMBINATORIA 46
Problema 45:
Dado un conjunto de 6 elementos distintos, calcular el número y formar todas las combinaciones ordinarias de cuarto orden.
SOLUCIÓN PROBLEMA COMBINATORIA 45
Problema 44:
Dadas cuatro vocales y cuatro consonantes distintas, calcular cuántas palabras de ocho letras pueden formarse, con la condición de que en cada palabra no aparezcan dos vocales ni dos consonantes seguidas.
SOLUCIÓN PROBLEMA COMBINATORIA 44-I
Problema 43:
Calcular la suma de todos los números de cinco cifras distintas que pueden formarse con los dígitos 1, 2, 3, 4 y 5.
SOLUCIÓN PROBLEMA COMBINATORIA 43
Problema 42:
Dado el conjunto {2, 4, 6, 8}, calcular cuántos números de cuatro cifras distintas pueden formarse con sus elementos.
SOLUCIÓN PROBLEMA COMBINATORIA 42
Problema 41:
¿Cuántos números de seis cifras distintas, existen en el sistema decimal?
SOLUCIÓN PROBLEMA COMBINATORIA 41
Problema 40:
¿Cuántos números de cuatro cifras distintas, mayores que 4.300, pueden formarse con los dígitos 1, 2, 3, 4, 5, 6 y 7?
SOLUCIÓN PROBLEMA COMBINATORIA 40
Problema 39:
¿Cuántos números de cuatro cifras distintas, menores que 5.000, pueden formarse con los dígitos 2, 4, 5, 7 y 8?
SOLUCIÓN PROBLEMA COMBINATORIA 39
Problema 38:
Un estudiante para aprobar un examen que consta de 10 preguntas, debe contestar 7 de ellas. ¿De cuántas maneras puede hacer la selección para aprobar el examen?
SOLUCIÓN PROBLEMA 38 COMBINATORIA
Problema 37:
Si en un colectivo hay 10 asientos vacíos. ¿De cuántas formas pueden sentarse 7 personas?
SOLUCIÓN PROBLEMA 37 COMBINATORIA
Problema 36:
Calcular el valor de
SOLUCIÓN PROBLEMA 36 COMBINATORIA
Problema 35:
Resolver la ecuación
SOLUCIÓN PROBLEMA 35 COMBINATORIA
Problema 34:
Resolver la ecuación
SOLUCIÓN PROBLEMA 34 COMBINATORIA
Problema 33:
¿Cómo comprobarías, sin hallar sus valores, que los siguientes números combinatorios son iguales?
SOLUCIÓN PROBLEMA 33 COMBINATORIA
Problema 32:
Hallar el valor de m para que se verifique:
SOLUCIÓN PROBLEMA 32 COMBINATORIA
Problema 31:
Hallar la suma de los números de combinaciones que pueden hacerse con 5 letras, tomadas primeramente dos a dos, después tres a tres, y después cuatro a cuatro.
SOLUCIÓN PROBLEMA COMBINATORIA 31
Problema 30:
Con las cifras del número 8.752.436, ¿Cuántas números distintos de tres cifras pueden formarse, no entrando repetida ninguna de ellas?
SOLUCIÓN PROBLEMA COMBINATORIA 30
Problema 29:
¿Cuántas combinaciones pueden formarse con las letras de la palabra manubrio, tomadas de tres a tres?
SOLUCIÓN PROBLEMA COMBINATORIA 29
Problema 28:
¿Cuántos objetos distintos tiene que haber para que el número de combinaciones que se puedan formar, tomándolos tres a tres, sea igual a 12 veces el número de objetos?
SOLUCIÓN PROBLEMA COMBINATORIA 28
Problema 27:
Con las cifras 1, 2, 3, 4 y 5, ¿Cuántos números distintos se pueden formar, con la doble condición de que entren todas en cada uno de aquéllos y la cifra 3 ocupe en todos el lugar de las centenas?
SOLUCIÓN PROBLEMA COMBINATORIA 27
Problema 26:
El séxtuplo del número de combinaciones que se pueden formar con m objetos, tomados tres a tres, es igual al número de variaciones que se pueden formar con m-1 objetos, tomados cuatro a cuatro. Deducir el valor de m.
SOLUCIÓN PROBLEMA COMBINATORIA 26
Problema 25:
¿De cuántas maneras distintas pueden colocarse 10 niños en un corro?
SOLUCIÓN PROBLEMA COMBINATORIA 25
Problema 24:
El número de combinaciones de x objetos, tomados 3 a 3, está, con el número de variaciones de los mismos objetos, tomados 2 a 2, en la relación ½. Calcular el número de objetos.
SOLUCIÓN PROBLEMA COMBINATORIA 24
Problema 23:
Una persona juega con 7 fichas de las 28 que tiene el dominó. ¿Cuántos juegos distintos pudiera llegar a tener?
SOLUCIÓN PROBLEMA COMBINATORIA 23
Problema 22:
El número de variaciones de m objetos, tomados dos a dos, multiplicado por el de combinaciones de otros m objetos, tomados también dos a dos, es 450. Calcular m.
SOLUCIÓN PROBLEMA COMBINATORIA 22
Problema 21:
Resolver la ecuación:
Siendo x≠4
SOLUCIÓN PROBLEMA COMBINATORIA 21
Problema 20:
En una fila de 10 butacas, ¿Cuántas posiciones diferentes pueden ocupar tres individuos?
SOLUCIÓN PROBLEMA COMBINATORIA 20
Problema 19:
A una persona se le sirve en cada comida cuatro platos, de lo nueve que son de su agrado. ¿Cuántas comidas diferentes puede hacer esa persona?
SOLUCIÓN PROBLEMA COMBINATORIA 19
Problema 18:
El número de variaciones de x letras diferentes, tomadas cuatro a cuatro, es al de variaciones, tomadas de cinco en cinco, como 1 es a 8. Hallar x.
SOLUCIÓN PROBLEMA COMBINATORIA 18
Problema 17:
Asisten a una clase 24 alumnos, y todos los días explican la lección dos de ellos. El profesor desea que los alumnos no sean los mismos ningún día. ¿Durante cuánto tiempo lo podrá conseguir?
SOLUCIÓN PROBLEMA COMBINATORIA 17
Problema 16:
¿Cuántos números enteros de cinco cifras, diferentes a 38426 y diferentes entre sí, se podrían formar con las cifras de ese número no entrando ninguna repetida?
SOLUCIÓN PROBLEMA COMBINATORIA 16
Problema 15:
Resolver la ecuación:
SOLUCION PROBLEMA COMBINATORIA 15
Problema 14:
Resolver la ecuación:
SOLUCIÓN PROBLEMA COMBINATORIA 14
Problema 13:
Con cinco clases de vino, tomadas dos a dos, ¿cuántas mezclas diferentes se pueden obtener, entrando igual cantidad de cada una de dichas clases?
SOLUCIÓN PROBLEMA COMBINATORIA 13
Problema 12:
¿Cuántas sumas diferentes, de dos sumandos, se pueden obtener con los números 1,3,5,11,21 y 41?
SOLUCION PROBLEMA COMBINATORIA 12
Problema 11:
Resolver la ecuación:
SOLUCIÓN PROBLEMA COMBINATORIA 11
Problema 10:
Resolver el sistema de ecuaciones:
SOLUCIÓN PROBLEMA COMBINATORIA 10
Problema 9:
¿De cuántas maneras diferentes pueden colocarse cuatro soldados en una fila?
SOLUCIÓN PROBLEMA COMBINATORIA 9
Problema 8:
Una palabra se compone de letras diferentes. ¿Cuántas serán éstas, sabiendo que el número de combinaciones de todas ellas, tomadas dos a dos, es el de combinaciones, tomadas tres a tres, como 3 es a 5?
SOLUCIÓN PROBLEMA COMBINATORIA 8
Problema 7:
¿Cuántas variaciones pueden formarse con 10 objetos, tomados tres a tres?
SOLUCIÓN PROBLEMA COMBINATORIA 7
Problema 6:
Hallar el número de permutaciones que se pueden formar con las letras de la palabra problema.
SOLUCIÓN PROBLEMA COMBINATORIA 6
Problema 5:
Con seis pesas de 1, 2, 5, 10, 20, 50 kilogramos, ¿cuántas pesadas diferentes pueden obtenerse, tomando aquéllas de tres en tres?
SOLUCIÓN PROBLEMA COMBINATORIA 5
Problema 4:
Un depósito de agua tiene 5 caños de desagüe, que arrojan 1, 3, 5, 10 y 20 litros por minuto. Abriendo indistintamente cuatro de estos caños, ¿en cuántos tiempos diferentes se puede desaguar el depósito?
SOLUCIÓN PROBLEMA COMBINATORIA 4
Problema 3:
Las cifras que componen un número, son 1, 2, 3, 4 y 5. ¿Cuántos números diferentes pueden contener todas ellas, con la condición de que ninguno sea mayor que 54000?
SOLUCIÓN PROBLEMA COMBINATORIA 3
Problema 2:
¿Cuántos números enteros y desiguales, mayores que 10 y menores que 100, se pueden formar con las ocho primeras cifras, no entrando repetida ninguna de ellas?
SOLUCIÓN PROBLEMA COMBINATORIA 2
Problema 1:
¿Cuántos productos diferentes pueden formarse con los números 7, 9, 11, 13 y 17, tomados de tres?